热红外图像去噪方法典型技术

1）帧间滤波

令f（x，y，k）为理想的无噪声图像，n（x，y，k）为成像过程中的噪声，I（x，y，k）为观测图像，（x，y）为图像像素位置，k为图像帧号。假设它们满足

帧间滤波为从时域角度对多帧图像，例如M帧，进行累加平均，即

假定f（x_，y，k）时域不变，n（x，y，k）是随机的，在时域上不相关，且均值为零，则I的期望和方差分别为

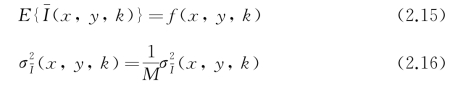
即I接近于理想状态下的无噪声图像f，且噪声方差显著减低，可见帧间滤波可以显著抑制静态图像噪声。但是，若热红外图像存在运动较快的目标时，简单应用帧间滤波会产生目标拖尾和边缘模糊，制约运动目标识别。为此，可以在检测运动快慢的基础上动态确定参与滤波的各图像帧的权重，由此改善热红外图像目标运动时的拖影问题。

2）（加权）邻域平均滤波

邻域平均滤波（或均值滤波）是一种线性滤波器，利用Box模板与图像进行卷积运算，实现对图像局部空间的平滑。Box模板中所有的系数相同且所有的系数之和为1。常用的Box模板尺寸有3×3、5×5等。

邻域平均滤波可表达为

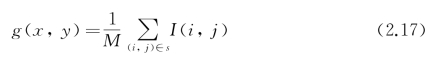
其中，I（x，y）和g（x，y）分别为源图像和去噪图像，s为以（x，y）点为中心点的图像局部邻域，M为该邻域中的像素点总数。

领域平均滤波计算简单，运行速度快，但去噪效果与模板大小密切相关。模板半径越大，滤波效果越好，但图像模糊程度越大，尤其在边缘和细节位置。因此，各类加权平均滤波为参与平均的像素点赋予不同权值，在平滑噪声同时保护边缘和细节。常用的加权平均法有灰度最近K邻点平均、梯度倒数加权平滑、最大均匀性平滑、小斜面模型平滑、高斯滤波等。

3）中值滤波

中值滤波将每一像素点的灰度值设置为该点某邻域窗口内的所有像素灰度的中值，通过使周围像素值接近真值消除孤立噪声点。在实现上，用某种结构的二维滑动模板，将模板内像素按照像素灰度值的大小排序，生成单调上升（或下降）的数据序列并取数据序列的中值元素作为输出，即

其中I（x，y）、g（x，y）分别为原图像和去噪图像；w为二维模板，通常为3×3、5×5等方形区域，也可以是线形、圆形、十字形、圆环形等其他形状区域，如图2.6所示。

图2.6　中值滤波常用窗口

中值滤波对脉冲干扰及图像扫描噪声十分有效，而且可以较好地克服线性滤波器所带来的图像模糊。为进一步提高性能或者面向某些复杂图像，可以使用复合型中值滤波，例如中值滤波线性组合、高阶中值滤波组合、加权中值滤波以及迭代中值滤波等［16］。

4）偏微分方程滤波

偏微分方程（partial differential equation，PDE）滤波模型源于物理学中的热扩散原理。对图像I（x，y）做线性热扩散滤波，等效于对I（x，y）做以时间t为尺度参数的高斯滤波。随着t的增大，图像边缘越来越模糊，最终收敛到图像均值［25］。

为实现去噪并达到保护图像边缘的目的，Perona与Malik提出了P-M模型［26］：

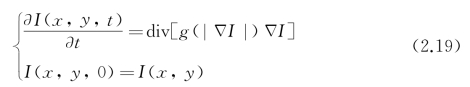
P-M模型的核心是引入边缘停止函数g（|I|）作为新的热传导率，使热扩散过程依赖图像局部梯度模值|I|，这样可将滤波和边缘检测相结合。g（|I|）具有快速单调下降特性。在图像平坦区，|I|→0，g（|I|）→1，扩散量大，平滑作用明显；在边缘位置，|I|→∞，g（|I|）→0，扩散几乎停止，平滑作用大大减弱。

P-M模型在数学上可能是不完善的。通过正则化，式（2.19）可修改为

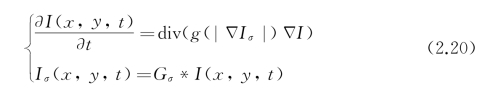
其中，Gσ是方差为σ的高斯函数。这就是CLMC模型［27］。

P-M/CLMC模型不约束扩散方向，在边缘切线和法线方向均会平滑边缘。为了在滤波过程中保护边缘，希望扩散只沿边缘切线方向进行，对应的PDE方程［28］为

其中，κ为局部曲率。式（2.21）表明图像沿边缘切线方向扩散等价于令图像的所有水平集做曲率运动。基于方向扩散可等价于图像水平集做某种运动的思想。Sapiro提出了图像所有水平集按测地线活动轮廓（geodesic active contour，GAC）模型［29］运动的模型，称为Self-Snake模型［30］。

GAC模型最小化式（2.22）能量泛函，实现对活动轮廓曲线的演化。

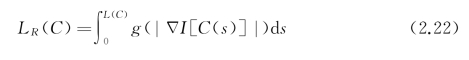
其中，C=（x（s），y（s））为曲线的矢量表示；s为曲线Euclidean弧长参数，s∈［0，max（L（C））］；L（C）为封闭曲线弧长；LR（C）为曲线的“加权”弧长；g（r）为边缘停止函数，参量r=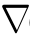Gσ*I。最小化式（2.22）对应式（2.23）梯度下降流：

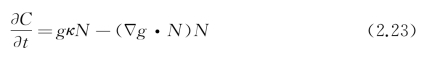
式（2.23）反映了在GAC模型中，曲线C的运动受到两种力的控制，一是来自曲线曲率运动的“内力”（右边第一项），当C位于边缘时其值会很小；另一种是源于Δ g的“外力”，它使得C向图像中目标边缘靠近并稳定在边缘上。式（2.23）对应的关于嵌入函数u的PDE为

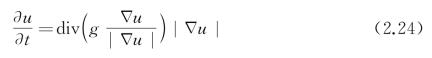
将图像I（x，y）作为嵌入函数u，得Self-Snake模型的PDE为

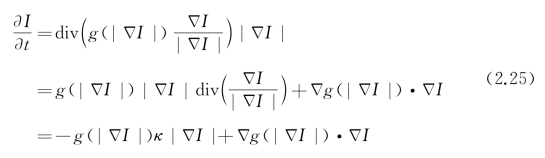(www.xing528.com)

图2.7展示了上述各滤波模型的去噪效果。线性滤波模型在滤除噪声时使目标区域严重扩散。CLMC模型采用边缘停止函数实现了滤波与边缘保护的结合，目标扩散被有效抑制，但不同边缘方向上抑制程度不一致。Self-Snake模型限制扩散只沿边缘切线方向发生，所以边缘在滤除噪声前后几乎没有变化。

图2.7　PDE模型去噪效果示例

5）小波阈值去噪

利用小波变换将图像从空间域变换到小波域，然后在小波域对小波系数做处理以减弱噪声，最后进行小波反变换得到去噪图像。在小波域，高频子带中较大的系数含有图像重要信息，且数目较少，大量较小系数主要包含噪声，且分布较为均匀。将小波系数与一个或多个阈值进行比较，依据比较结果对小波系数置零、保持或收缩，能够降低噪声，同时保留图像细节。

小波阈值去噪中使用的阈值处理函数包括硬阈值函数、软阈值函数以及另外一些改进的阈值函数，如半软阈值函数、Minimax阈值函数、Garrote阈值函数。令w表示小波系数，T表示阈值，这些阈值函数的数学表达式为

（1）硬阈值函数

（2）软阈值函数

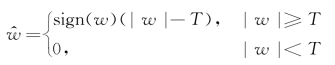
（3）半软阈值函数

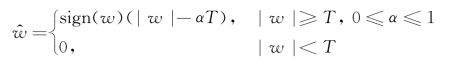
（4）Minimax阈值函数

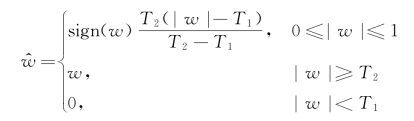
（5）Garrote阈值函数

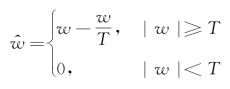
硬阈值函数能够较好地保留图像的纹理和边缘等细节，但视觉效果上会产生人为噪点，使图像有一定的失真现象。软阈值函数获得的图像在视觉效果上比较平滑，但可能损伤图像的细节信息，使去噪图像模糊。半软阈值函数在α取0和1时分别退化为硬阈值函数和软阈值函数，但当α≠1时，处理后系数不具备连续性。Minimax阈值函数在双阈值T1和T2中添加了噪声与信号间的过渡区，符合自然信号的连续特性。Garrote阈值函数本身具有连续性，能较好地克服硬阈值与软阈值函数各自的不足［31］。

合理估计阈值T是小波阈值去噪的关键。常用的阈值估计准则有VisuShrink［32］、BayesShrink［33］、BiShrink［34］、BlockShrink［35］、NeighShrink［36］等。其中，VisuShrink是一种通用的阈值选取规则。它假定小波系数是独立的，且噪声服从正态高斯分布，并采用单一阈值处理所有小波系数，其阈值估计表达式为

其中，σ为噪声标准差；M×N为图像尺寸。由于VisuShrink对全部高频子代系数进行同一阈值处理，往往使去噪图像过度平滑，图像细节保留不够。

为使阈值具有自适应的特性，BayesShrink在假设无噪图像的小波系数服从广义高斯分布的前提下，通过最小化贝叶斯风险函数得到一个可根据图像统计特性自适应调整的最优阈值，并经过软化处理，获得较好的去噪效果。BayesShrink的阈值估计表达式为

其中，σX为广义高斯分布的标准差；σ⌒2为噪声方差，可利用第一高频子带系数按式（2.28）估计获得。

其中，median为取中值操作。BayesShrink的缺点是仍然没有考虑到系数间的相关性，因此BiShrink、BlockShrink、NeighShrink等以不同方式进一步考虑小波系数间的相关性以改善去噪效果。

小波变换使得图像能量集中在一些大的小波系数上，而噪声能量却分布在整个小波域。由于不同小波变换的这种变换能力不同，因此对小波变换类型的选择对去噪效果同样关键。如图2.8（a）所示，传统二维离散小波变换（2D DWT）使用行列可分离的滤波器对输入数据的行和列依次进行一维分解，并反复递归构成金字塔结构的二维小波分解。图2.8（b）显示了2D DWT在垂直、水平、对角三个方向上的小波图像，可见任意方向上均有明显的马赛克，且对角方向无法区分±45°。图2.9（a）中，一维（1D）双树复小波变换（DTCWT）引入两个DWT构建起双树结构，其中A树给出DTCWT的实部，B树给出DTCWT的虚部。2D DTCWT是1D DTCWT的扩展，也是行列可分离的。图2.9（b）显示了2D DTCWT的6个复小波图像，由此实现了对±15°、±45°、±75°六个主方向的描述，且马赛克明显减弱［37］。

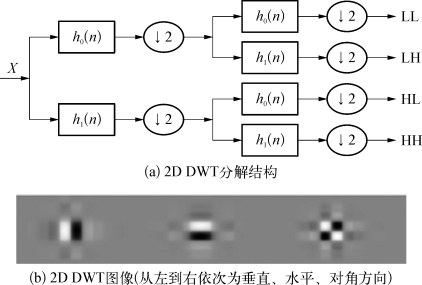
图2.8　一级二维离散小波变换

一般地，经典DWT具有多分辨率分析、完全重构、运算复杂度低以及稀疏表征等优点，同时存在小波系数正负振荡、缺乏平移不变性、频谱混叠和方向性差的不足。作为DWT的改进，双密度小波（DDWT）基于一个尺度函数和两个小波函数，获得了近似的平移不变性、完全重构性和有限的冗余性优势。由于每个方向都有两个小波描述，增加了图像描述的信息量。双树复小波变换（DTCWT）同样克服了DWT的缺点，在具有传统小波优良时频局部化能力的同时具有了平移不变性和良好的方向选择性。双密度双树复小波变换（DD-DTCWT）进一步综合了双密度小波和双树复小波的优点，对图像的细节描述更加精确，应用于热红外图像去噪，理论上能够提升去噪质量。

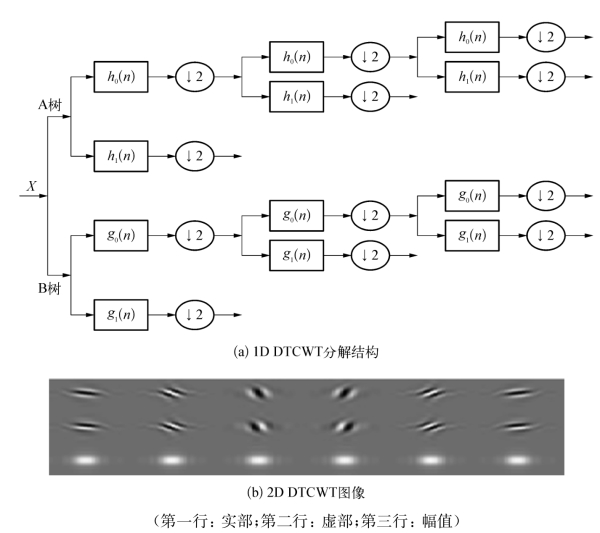
图2.9　一级二维双树复小波变换

6）多尺度几何分析去噪

X-let多尺度几何分析工具与小波分析相比实现了对图像的更高效稀疏表达，即图像信息在变换域会更加集中于少量系数，有利于图像信号与噪声的分离。同时，同一尺度下具有更多方向子带，联合多个子代系数特征能够更加精准地识别噪声。因为一般认为在所有子带中幅度均较大的变换系数对应图像的强边缘，某些方向子带中幅值较大但在同一尺度下其他方向子带中幅值又较小的变换系数对应图像的弱边缘，在所有子带中幅值均是小值系数对应于噪声，这样的特性为去噪提供了前提［38］。

热红外图像同时具有强噪声与弱边缘特性，而利用多尺度几何分析可以自然实现对图像的去噪和增强，因而在图像预处理中具有明显优势。

多尺度几何分析去噪的一般步骤为：

（1）对红外图像进行多尺度几何变换，得到多尺度、多方向子带系数；

（2）分析不同子带中系数的特征并作相应处理。例如对于强边缘系数应保持，弱边缘系数应放大（或保持），将噪声系数归零；

（3）多尺度几何分析逆变换，获得去噪图像。