热红外图像增强方法及人体目标检测

图像增强是通过对图像数据的加工，增强图像中用户感兴趣的信息，达到改善图像视觉效果以及便于计算机处理的目的［15］。尽管图像增强不增加图像数据中的信息，但会扩充边缘、轮廓、对比度等特征的动态范围，使得对这些特征的检测和识别变得更加容易。由于热成像固有的特性，热红外图像的质量普遍较低，因此对图像进行增强处理往往是必要的。

热红外图像增强方法包括空域方法和变换域方法。空域方法是在图像的像素空间对每个像素点进行操作，通过修正像素灰度值达到增强的目的。变换域方法是修改图像在某种变换域内的参数，以达到增强变换域特征的目的，再经逆变换到像素空间得到增强图像。具体增强方法的选用应根据图像特点与应用需求而定。

1）灰度变换（gray-level scale transform，GST）

图像中像素灰度的最大值与最小值之比称为对比度。热红外图像很多时候具有对比度低的特点，所以改善对比度是热红外图像增强的重要内容。

灰度变换利用变换函数直接调整像素灰度，达到扩大动态范围、改善对比度的目的。它的基本思想可表述为其中，s和r分别为变换后和变换前的像素灰度值；T代表变换函数，常用的有（分段）线性函数、对数函数、幂律（Gamma）函数（n次幂和n次根）等。图2.1展示了利用分段线性变换函数实现的图像增强效果。该示例中，图像被划分为目标区、过渡区和背景区。利用分段线性变换，拉伸目标区灰度范围，保持过渡区灰度范围，压缩背景区灰度范围，以此达到增强对比度的目的。

图2.1　热红外图像的分段线性变换增强

总体上，灰度变换直接处理图像的像素，在操作上具有简单易行的优点，缺点是难以适应复杂场景，而且变换函数的参数也不易确定，因此只适用于要求较低的场合。

2）直方图均衡（histogram equalization，HE）

灰度直方图是反映图像灰度级与出现这种灰度级的概率之间关系的图像。灰度直方图可以提供多种信息，例如图像灰度动态范围，每个灰度级上像素出现的概率，图像的整体对比度以及平均明暗情况。图2.2显示了一些热红外图像的灰度直方图，容易看出这些热红外图像具有以下特点［16］：

（1）像素灰度动态范围不大，很少充满整个灰度级空间；

图2.2　典型热红外图像的直方图［9］

（2）多数情况下呈现单峰或双峰（分为主、次峰）；

（3）绝大部分像素集中于某些相邻灰度级范围，这些范围以外的灰度级上没有或只有很少的像素。

直方图均衡是一种广泛采用的图像增强方法。通过把源图像的灰度直方图变换为整个灰度范围内的近似均匀分布、扩大灰度动态范围来提升图像对比度，其工作步骤如下。

（1）计算源图像的灰度直方图i=0，1，…，L-1，其中ni为图像中灰度为k的像素点数，n为图像像素总数，L为灰度级数。

（2）计算累计直方图

（3）利用灰度变换函数计算变换后的灰度值：j=int［（L-1）p（j）+0.5］^[1]。

（4）确定灰度变换关系，将源图像f（m，n）=i修正为g（m，n）=j。

（5）重新计算变换后图像的灰度直方图。

图2.3（a）和（b）展示了直方图均衡的增强效果。可见经过增强，图像动态范围扩展到整个灰度区间，对比度显著提升。值得注意的是，热红外图像具有背景强、目标弱小的特点，面积较小的目标在图像增强处理后可能会“淹没”在面积较大的背景中，这样可能反而降低了目标与背景之间的对比度。因此，出现了诸如平台直方图均衡（plateau histogram equalization，PHE）［17］、自适应平台直方图均衡（adaptive plateau histogram equalization，APHE）［18］等改进方法。这些方法通过将直方图分段或设置阈值，弥补了改善图像细节丢失及过度增强的不足。

3）遗传算法

遗传算法是一种基于自然选择理论的宏启发式算法。它利用选择、交叉、变异等遗传操作算子来生成或搜索种群中更高质量的解，以实现对问题的最优求解［19］。

遗传算法可以较好地实现热红外图像增强，其实质是寻找一种灰度变换关系。遗传算法首先对输出图像与输入图像的灰度对应关系进行编码，并随机初始化此灰度对应关系（即初代个体），然后根据一定的图像质量评价标准构造适应度函数，再反复利用遗传操作（包括变异、交叉、选择）进化生成新的后代个体，直到满足优化准则，这样就找到了最优或者近似最优的灰度变换关系，并最终应用这种关系实现图像增强。图2.3（c）给出了遗传算法对图2.3（a）的增强结果，可见效果较为理想。

图2.3　红外图像增强实例

构建合理的适应度函数是遗传算法获得高质量解的关键。另外，遗传算法要注意解决计算量过大的问题，因为面向问题可能设置较大的种群规模并经历较长的进化过程才能搜索到解［20］。

4）模糊算法

通常情况下热红外图像由于对比度较低，灰度变化缓慢，前景区域和背景区域的分界模糊，并不容易区分。模糊算法即利用模糊集理论模仿人类处理不确定性信息的优势，能够很好地适应热红外图像的这种不确定性。

热红外图像的模糊增强的一般步骤如下：

（1）将图像从空间域变换到模糊域；

（2）在模糊域修改前景和背景区的特征，实现模糊增强；

（3）将模糊特征映射回图像平面获得增强图像。

现以Pal-King模糊算法［21］为例加以说明。首先，将目标区域定义为一个模糊集合，图像中每个像素都有其隶属度，隶属度数值越大，说明其越属于目标区域。令像素属于目标区域的隶属度为μmn，按式（2.2）可将图像从空域转换到模糊域。

其中，gmn为像素灰度；gmax为图像最大灰度；Fd和Fe为模糊因子。

可按式（2.3）修改隶属度：

即利用指数函数将大于0.5的隶属度值增大，将小于0.5的隶属度值减小，以此降低模糊性。为进一步降低模糊性，可进行多次自身调用，即

(www.xing528.com)

以得出最佳模糊映射值。最后，通过模糊逆变换

得到空域灰度值。图2.3（d）是图2.3（a）的模糊增强结果，可见增强效果较好。

5）傅里叶分析法

傅里叶分析法首先将图像通过傅里叶变换转移到频域，然后在频域使其与一个滤波函数相乘以改变原图像的频域分布，最后将相乘结果通过傅里叶反变换获得增强图像。

设图像f（x，y）的尺寸为M×N，二维傅里叶变换与反变换定义为

若直接按上述定义对图像进行变换，计算效率太低。实践中通常使用其快速算法，即快速傅里叶变换（fast Fourier transform，FFT）和快速傅里叶反变换（inverse fast Fourier transform，iFFT）。这样，傅里叶分析增强的一般性表达为

其中，FFT、iFFT分别是快速傅里叶变换及快速傅里叶反变换；H（u，v）为滤波函数，按不同的增强目的，H（u，v）可以为低通滤波、高通滤波、带通/带阻滤波函数等［15］。

6）小波分析法

小波变换是一种优越的多分辨分析方法，具有时频局部化和多分辨率特性，能够同时进行时域和频域分析。利用小波变换可以精细分析图像成分，在增强图像对比度、边缘等特征时有效地抑制图像噪声。

对任意图像f（x，y），其小波分解为

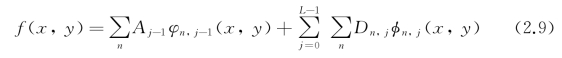
其中，图像函数f∈Vj，｛Vj，j∈Z｝是L2（R）上的一个多分辨率分析，φ和φ分别为相应的小波函数和尺度函数，Aj-1为低频系数，Dn，j为高频系数。低频系数反映了图像的基本面貌，高频系数体现了图像不同方向上的细节。图2.4展示了图像的多尺度小波分解系数结构。

图2.4　图像的多尺度小波分解系数结构

基于小波分析的图像增强一般步骤如下：

（1）将原图像进行小波变换，得到不同尺度、不同方向的分解系数；

（2）根据增强目的，计算增益系数，以此修改不同尺度、不同方向上小波分解系数，使得某些感兴趣的分量被放大且某些不需要的分量被减小；

（3）基于修改后的小波分解系数，经小波反变换得到增强图像。

步骤（2）中的系数修改方式主要有高频加强、反锐化掩模以及子带增强。高频加强是通过整体提升高频系数，相对突出图像高频成分，使得图像边缘增强，但因所得图像往往偏亮或偏暗，对比度可能变差，需要小波反变换后再进行对比度增强，获得高质量增强图像，如图2.5所示。

图2.5　基于小波分析的图像增强实例

反锐化掩模是将图像进行模糊预处理（相当于低通滤波）后与原图像求差，差值图像乘上一个修正因子后再与原图像求和，以达到增强图像边缘的目的。基于小波变换实现反锐化掩膜相比传统方法有明显的优越性。首先，小波变换使原图像中不同分辨率的细节特征随尺度不同而分离，避免了传统方法中需要不断调整低通滤波器窗口来选择增强效果的烦琐工作。其次，由于是对不同尺度下的小波系数分别进行增强，原图像中不论较粗还是较细的边缘都能得到增强。

子带增强则是将图像做小波分解后对各个分解层进行线性运算，一般是将需要的子带系数与增益系数相乘，最后通过小波逆变换精确重建图像。在子代增强中，最优的小波分解层数以及增益系数的确定对增强质量有显著影响。

7）多尺度几何分析法

脊波（ridgelet）变换、曲波（curvelet）变换、轮廓波（contourlet）变换、条带波（bandelet）变换、楔波（wedgelet）变换、小线（beamlet）变换等统称为X-let多尺度几何分析工具，它们能够实现对图像的高效稀疏表达［22］。以contourlet变换为例，它能用比小波变换更稀疏的长条形基来表示图像边缘轮廓，并可以在同一尺度下产生更多方向子带（相较之下离散小波变换每一级只有三个细节子带），因此对图像成分的表达比小波变换更精细。

利用多尺度几何分析实现图像增强，首先对图像进行多尺度多方向分解，然后用增强算子对各个子带系数做增强处理，最后经相应逆变换得到增强图像。

8）视网膜大脑皮层（Retinex）模型

Retinex理论认为物体的颜色由物体对不同波段的反射能力决定。物体具有色彩一致性，光照均匀与否并不影响物体的色彩。热红外图像属于灰度图像，尽管成像机理与可见光图像不同，但是类比可见光图像成像的机理，可以假设物体发出的红外辐射是在红外光源照射下物体对红外光线的反射，而热红外图像就是由物体反射的红外光线所形成的，这样Retinex理论也适于处理热红外图像，只是在处理时仅存在一个颜色通道，区别于彩色图像的三个颜色通道［20］。

令观测图像为f（x，y），反射图像为R（x，y），照度图像为L（x，y），依据Retinex理论，f（x，y）可分解为R（x，y）和L（x，y），其中R（x，y）被认为是不受外界影响的理想图像，而L（x，y）可视为光照不均匀，是影响图像质量的主要因素。反映这三者关系的数学模型为

模型将照度图像视为附加在理想图像上的乘性噪声。去除该噪声对观测图像的影响即可达到图像增强的目的。

经典单尺度Retinex图像增强算法（single-scale Retinex，SSR）中将式（2.10）转换到对数空间求解R（x，y），即

其中，“*”表示卷积运算，G（x，y）表示标准环绕函数，即

其中，σ为环绕邻域的标准差，ω为归一化因子。

基于式（2.11），SSR将原图像减去标准环绕函数与观测图像的卷积值，使得原图像被减去慢变化部分，且σ参数值越小，图像慢变化成分减去越多，剩余图像中的快变化成分越多，从而越能突出原图像细节。对于图像中存在的严重暗区，SSR可以明显增强其细节［23］。

在SSR基础上，多尺度加权平均Retinex（multi-scale Retinex，MSR）、带彩色恢复的多尺度Retinex（multi-scale Retinex with color restoration，MSRCR）等Retinex改进方法可以进一步提升增强效果。