数学故事第9册|挡板法与放球问题解析

我们常常遇到（或可化为）下列问题：求方程x1 ＋x2 ＋…＋xm ＝n（m，n为正整数，m ≤n）的正整数解的个数。上述不定方程正整数解的个数问题可以转化为下列数学模型：把n个相同的小球排成一行，并将它分成m 段，每一段至少一个小球，有几种分法？

解：因为将一行球分成m 段，只要用m－1隔板将小球分隔，又n 个小球产生n－1空位（不计两端的两个空位）。取m－1块隔板，在这n－1个空位中任选m－1个位置放置这m－1块隔板，共有 种放法。

因此，方程x1＋x2＋…＋xm ＝n（m，n为正整数，m ≤n）的正整数解的个数为

【推论1】方程x1＋x2＋…＋xm ＝n（m，n 为正整数，m ≤n）的非负整数解的个数为

证：原方程等价于（x1＋1）＋（x2＋1）＋…＋（xm ＋1）＝n＋m，令yi＝xi＋1（i＝1，2，…，m），则y1＋y2＋…＋ym ＝n＋m，这里yi ≥1（i＝1，2，…，m），故方程x1＋x2＋…＋xm ＝n 的非负整数解的个数等于方程y1＋y2＋…＋ym ＝n＋m 的正整数解的个数，为

【例7】将n＋1个不同的小球放入n 个不同的盒子里，要求每个盒子不空，共有多少种不同方法？

解法1：因为每个盒子不空，所以应当有一个盒子里放入2个小球，而其他每个盒子里放入1个小球，对该事件作如下分步：（1）从n 个不同的盒子中选1个来放2个球，方法数为（2）从n＋1个不同的小球中选出2个小球来放入选出的盒子，方法数为（3）将余下的不同小球放入剩下的不同盒子里（每个盒子放入1个小球），方法数为故完成该事件的方法数为

解法2：（1）将这n＋1个小球排成一排，方法数为（2）在两两之间的n 个间隔之间插入n－1块隔板，方法数为由于有两个小球处在两个隔板之间且不计较顺序，所以完成题目所给事件的方法数为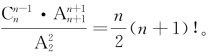

解法3：对该事件作如下分步。

（1）从n＋1个不同的小球中选出n 个小球放入n 个盒子里，每个盒子放1个，有不同放法；（2）将剩下的一个小球放入n个盒子中的一个，有不同放法n 种，由于当“甲，乙两球放在同一个盒子里时”，“甲先放入（排列时放入的）、乙后放入”与“乙先放入（排列时放入的）、甲后放入”是同一种放法，所以完成题目所给事件的方法数为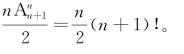

下面选取几例典型的试题参考。(www.xing528.com)

【例8】（2010年全国联赛）求方程x＋y＋z＝2 010满足x ≤y ≤z 的正整数解（x，y，z）的个数。

解：首先易知x ＋y＋z＝2 010的正整数解个数为2 009×1 004，把x＋y＋z＝2 010满足x ≤y ≤z 的正整数解分为三类：

（1）x，y，z 均相等的正整数解的个数显然为1；

（2）x，y，z 中有且仅有2个相等的正整数解的个数，易知为1 003；

（3）设x，y，z 两两均不相等的正整数解为k，由排列易知1＋3×1 003＋6k＝2 009×1 004，6k＝2 009×1 004－3×1 003－1解得k＝335 671。从而满足x ≤y≤z的正整数解的个数为1＋1 003＋335 671＝336 675。

如何研究方程x1＋x2＋x3＋…＋xk ＝n（且x1 ≥1，x2 ≥2，…，xk ≥k）的正整数解的问题？换元法：令yi ＝xi－（i－1），1≤i≤k，则转化为y1＋y2＋y3＋…＋yk ＝n－（1＋2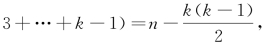＋又转为求正整数解的个数问题。

【例9】（2005年全国联赛）若自然数a 的各位数字之和为7，则称a 是“吉祥数”。将所有“吉祥数”从小到大排成一列：a1，a2，a3，…，若an ＝2 005，则a5n＝________。

解：∵方程x1＋x2＋x3＋…＋xk＝m 的非负整数解的个数为而使x1≥1，ｘi≥0（i≥2）的整数解个数为现取m＝7，可知k 位“吉祥数”的个数为∵2005是形如的数中最小的一个“吉祥数”，且对于四位“吉祥数”1abc，其个数为满足a＋b＋c＝6的非负整数解的个数，即故2005是第1＋7＋28＋28＋1＝65个“吉祥数”，即a65 ＝2 005，5n＝325。又

而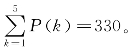

∴从大到小最后6 个五位“吉祥数”是：70 000，61 000，60 100，60 010，60 001，52 000，∴第325个“吉祥数”是52 000，即a5n ＝52 000。