二元一次不定方程整数解求解法

这里讨论的二元一次不定方程专指ax ＋by＝c（ab ≠0，a，b，c为整数）。

【定理1】二元一次不定方程ax＋by＝c有整数解，当且仅当整数a 和b的最大公约数（a，b）整除c。

证明　设（a，b）＝d。

充分性：因为d＝（a，b），所以存在整数x0，y0 使ax0 ＋by0＝d，又d｜c，所以c＝dk＝k（ax0＋by0）＝a（kx0）＋b（ky0），所以方程ax ＋by＝c有整数解（kx0，ky0）。

必要性：因为ax0＋by0＝c，x0，y0 为整数。

d 是a，b 的最大公约数，所以d｜a，d｜b，故d｜ax0＋by0，即d｜c。

如：方程2x ＋4y ＝5 没有整数解；2x ＋3y ＝5 有整数解。

【定理2】若整数a，b 互质，则方程ax ＋by ＝1有整数解，同时方程ax ＋by ＝c 也有整数解。若（x0，y0）是方程ax ＋by＝1的一个整数解，则cx0，cy0 是方程ax ＋by＝c 的一个整数解。

【定理3】整系数方程ax＋by＝（a，b）有整数解。

定理2和定理3都是“裴蜀定理”的内容。

【定理4】如果是满足整系数方程ax＋by＝c的一组整数解，则（其中u 为任意整数）也是满足上式的整数解。

这表明，满足方程的整数解有无穷组，并且在ab＞0时，可选择x 为正（负）数，此时y 相应地为负（正）数。这个结论可以通过把这组解直接代入已知方程进行证明。

由这个定理，只要能够观察出二元一次方程的一组整数解，就可以得到它的全部整数解。

例如，方程4x＋5y＝21的一组解为则此方程的所有整数解可表示为：

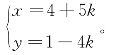
【定理5】n 元一次不定方程a1 x1＋a2 x2＋…＋an xn＝c（其中a1，a2，…，an，c为整数）有解的充要条件是最大公约数（a1，a2，…，an）｜c。

解n 元一次不定方程a1 x1＋a2 x2＋…＋an xn ＝c的方法：

可先顺次求出（a1，a2）＝d2，（d2，a3）＝d3，…，（dn－1，an）＝dn，若dn｜c，则方程无解；若dn｜c，则方程有解，作方程组：

求出最后一个方程的一切解，然后把tn－1 的每一个值代入倒数第二个方程，求出它的一切解，这样下去即可得方程的一切解。不定方程通常有无穷多的解。

【例1】求3x＋21y＝118的整数解。

解：由于3与21的最大公约数（3，21）＝3，而118不能被3整除，故方程无整数解。

【例2】求24x ＋17y＝1的一组整数解。

解法1：

7＝24－17×1

结果　1＝5×（24－17×1）－17×2

＝5×24－7×17

24×5＋17×（－7）＝1

24x＋17y＝1特殊解

（x，y）＝（5，－7）

解法2：用同余解决。

24x＋17y＝1　①

24x ≡1（mod17）

又24x ≡7x（mod17）

7x ≡1（mod17）

设7x＝17k＋1（k 是整数）　②(www.xing528.com)

17k ≡－1（mod7）

∵17k ≡3k（mod7）

3k ≡－1（mod7）

3k＝7t－1（t是整数）　③

在③中令t＝1，k＝2

由②x＝5

由①y＝－7

24x＋17y＝1的特殊解是（x，y）＝（5，－7）。

【例3】求36x ＋83y＝1的整数解。

解：用辗转相除法求解。

1＝3－2＝3－（11－3×3）

＝4×3－11

＝4×（36－3×11）－11

＝4×36－13×11

＝4×36－13×（83－2×36）

＝30×36－83×13

显然x ＝30，y＝－13是一组解（特解）。

因此，方程的通解为：x ＝30－83t，y＝－13＋36t。

【例4】装某种产品的盒子有大、小两种，大盒每盒能装11个，小盒每盒能装8个，要把89个产品装入盒内，要求每个盒子都恰好装满，需要大、小盒子各多少个？

解：奇偶法。设需要大、小盒子分别为x、y 个，则有11x ＋8y＝89，由此式89为奇数，8y 为偶数，所以11x 一定为奇数，所以x 一定为奇数，经计算得大、小盒子各3、7个。

【例5】有271位游客欲乘大、小两种客车旅游，已知大客车有37个座位，小客车有20个座位。为保证每位游客均有座位，且车上没有空座位，则需要大客车多少辆？

解：尾数法。大客车需要x 辆，小客车需要y 辆，可列出方程：37x＋20y＝271，20y 的尾数一定是0，则37x 的尾数等于271的尾数1，x 只能是3。

【例6】求方程组的正整数解。

解：两式相减：7x ＋5y＝36

得：

故1－2x 须为5 的倍数，而1－2x 为奇数，故1－2x ＝5（2k＋1）

得：x ＝－（5k＋2）

y＝7＋5k＋2＋2k＋1＝7k＋10

z＝36－x－y＝36＋5k＋2－7k－10＝－2k＋28

解须为正整数，则－（5k＋2）＞0，得：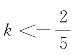

7k＋10＞0得：

－2k＋28＞0，得：k ＜14

显然k＝－1，故方程组有1组正整数解（x，y，z）＝（3，3，30）。