圆内接四边形对角线垂直，婆罗摩笈多的几何工作和面积公式

【定理1】若圆内接四边形的对角线相互垂直，则垂直于一边且过对角线交点的直线将平分对边。

如图，圆内接四边形ABCD 的对角线AC⊥BD，交点为M，EF⊥BC，且M 在EF 上，那么F 是AD 的中点。

【证明1】

如图，∵AC ⊥BD，ME ⊥BC，

∴∠CBD ＝∠CME，

∵∠CBD ＝∠CAD，∠CME ＝∠AMF，

∴∠CAD ＝∠AMF，

∴AF＝MF，

∵∠AMD＝90°，由直角三角形斜边中线定理逆定理可知，F是AD 中点。

【证明2】运用向量证明。

∵B、F、A 共线，由共线向量基本定理可知，存在唯一实数k，使

kEA·EC＝（1－k）EB·ED

∵EA·EC＝EB·ED（相交弦定理）

∴k＝1－k，k＝1/2

∴，即F 是BA 中点。

婆罗摩笈多还推广了关于三角形面积的海伦公式，导出了圆内接四边形的面积公式。

【定理2】求圆内接四边形的面积。

【证明1】

【证明2】

记△ABC 的面积为［ABC］，其余同。

如果一个四边形既有外接圆，又有内切圆，称之为双心四边形。

【定理3】若双心四边形四边依次为a、b、c、d，则面积A 为

【证明】(www.xing528.com)

【例1】任意△ABC，以两边作正方形ACHG、ABIF，连GF，反向延长△ABC 垂线AD 交GF 于E，求证：E 为GF 中点。

【证明】连结BE，CE，

∵AD ⊥BC，

∴BE2－BA2＝CE2－CA2，

BE2＝AB2＋AE2－2AB·AE cos∠BAE，

CE2＝AC2＋AE2－2AC·AE cos∠CAE，

∴AC·AE·cos∠CAE ＝AB·AE·cos∠BAE，

∵AC＝AG，AB ＝AF，

∴AG·cos∠CAE ＝AF·cos∠BAE，

∵sin∠GAE ＝－cos∠CAE，sin∠FAE ＝－cos∠BAE，

∴AG·sin∠GAE ＝AF·sin∠FAE，

即［AEF］＝［AEG］，

即E 为FG 的中点。

【例2】已知一个平面四边形的四条边长依次为2，3，3，6，求这样的四边形面积S 的最大值。

【解】由题意，四边形ABCD 的边长分别为AB＝2，BC＝3，CD＝3，DA＝6，连接BD，则由余弦定理可得BD2＝22＋62－2·2·6·cos A ＝32＋32－2·3·3·cos C，

故有

又因为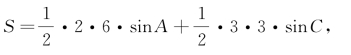

故有

由①、②两边平方相加可得

4S2＋112＝122＋92－2·12·9·cos（A ＋C）≤122＋92＋2×12×9，

解得其中，当且仅当cos（A ＋C）＝－1，

即四边形ABCD 对角互补（四边形是圆内接四边形）时，S 取最大值