数值计算方法第3版：龙格⁃库塔法

从上面的过程可见，因为要计算若干偏导数的值，所以用Taylor 展开式多展开几项来提高方法的阶数并不现实。 为了避免计算高阶导数，下面介绍龙格⁃库塔方法的思想，即利用f（x，y）某些点处的值的线性组合构造计算公式，使其按泰勒公式展开后与初值问题解的泰勒展开式比较，有尽可能多的项相同。

考虑离散化公式（8.6）：yi＋1 ＝yi＋hΦ（xi，yi，h），i＝0，1，…，n－1，y0 ＝a。

在y（x＋h）的Taylor 展开式中，取p ＝2 得

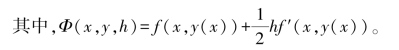
又根据复合函数求导法则有

所以

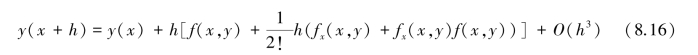
另一方面，令

其中，

这里c1，c2，λ2，μ21为待定系数。

将K2 展开成

则式（8.17）可写成

因此

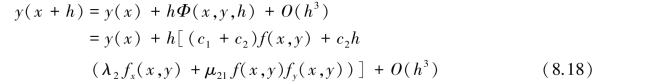
比较式（8.16）和式（8.18）两式，得

(www.xing528.com)

该方程组有四个未知量，但只有三个方程，故有无穷多组解。 令c2 ＝a≠0，则得这样取定参数a 得到的公式统称为二阶龙格⁃库塔（Runge⁃Kutta）方法。 其一般形式为

可以验证二阶龙格⁃库塔公式的局部截断误差都是O（h3），故二阶龙格⁃库塔方法都是二阶方法。

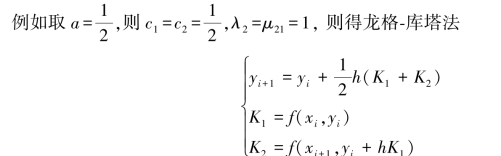
它就是改进的欧拉方法（8.15）。

或

式（8.21）称为中点方法。

龙格⁃库塔法的一般形式为：

常用的四阶（经典）龙格⁃库塔法如下：

四阶（经典）龙格⁃库塔方法的每一步需要计算四次函数值f，可以证明其局部截断误差为O（h5）。

例8.4　用四阶龙格⁃库塔法求例8.1（x∈［0，0.7］ ，取h ＝0.1）的数值解。

解　由式（8.23）得

计算结果见表8.3。

表8.3　计算结果