改进欧拉方法-数值计算方法第3版

由微分方程数值解的三种基本构造方法知，若取不同的差商（如向后差商），不同的数值积分公式（如梯形公式），以及泰勒公式取前三项、四项等可得不同的算法。

如果用向后差商近似代替导数，则有

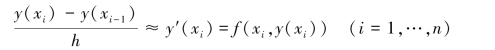
即

所以有

式（8.11）称为隐式欧拉公式。

如果用梯形公式计算积分：

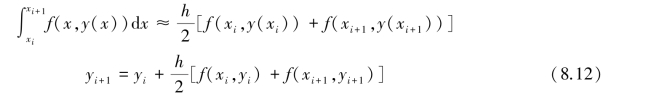
且

称式（8.12）为梯形方法。

由于此方程为yi＋1的隐式方程，不易求解。 一般将其与欧拉方法联合使用，可得梯形方法的迭代公式为

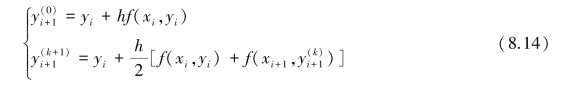
可以证明迭代过程（8.14）是收敛的。 事实上，将式（8.12）与式（8.14）相减，得

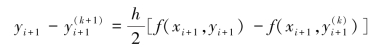
于是

按式（8.14）计算初值问题（8.1）的数值解时，虽然提高了精度，但其算法复杂：每迭代一次，都要重新计算函数f（x，y）的值，计算量很大，而且往往难以预测。 为了控制计算量，通常只迭代一两次就转入下一步的计算，这就简化了算法。

例8.1　用欧拉方法求解初值问题

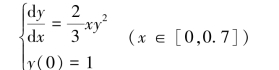
（取h ＝0.1）。

解　由欧拉方法（式（8.9）），取h ＝0.1，得数值计算公式

(www.xing528.com)

因为y0 ＝y（0）＝1，所以

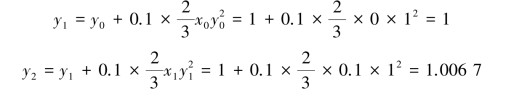
依次可计算出y2，y3，…， y6。

该初值问题的解析解为（x2－3）y ＝－3，由此可得到用欧拉方法求解的误差。 计算结果见表8.1。

表8.1　计算结果

例8.2　用欧拉法、改进欧拉法求解初值问题

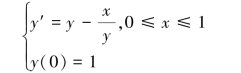
取h ＝0.1 计算。

解　取h ＝0.1，由欧拉方法（式（8.9）），得数值计算公式

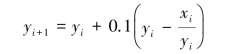
由改进的欧拉方法（式（8.15）），得数值计算公式

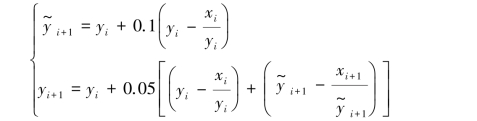
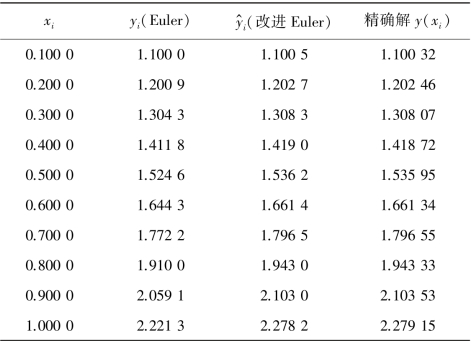
把用欧拉方法的计算结果记为yi，用改进的欧拉方法的计算结果记为y＾i，并把该初值问题的解析解y2 ＝0.5e2x＋x＋0.5 的计算值记为y（xi），则计算结果如表8.2 所示。

表8.2　计算结果

例8.3　讨论改进欧拉法的精度。

解　对于改进的欧拉法（8.15），当yi ＝y（xi）时，由二元函数的Taylor 公式得

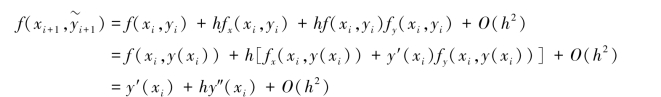
于是

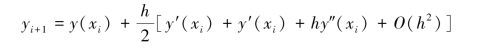
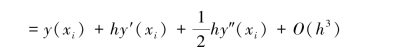
而由式（8.5）有

比较得　

因此，改进欧拉法是二阶方法。