数值计算方法第3版：迭代法解线性方程组

考虑线性方程组

其中A 为非奇异矩阵。 当A 为低阶稠密矩阵时，前面介绍了解线性方程组的直接法（例如选主元的高斯消去法等）。 但是对于工程技术中产生的大型稀疏矩阵方程组，则利用迭代法求解是合适的。 在计算机内存和运算两方面，迭代法通常可利用A 中有大量零元素的特点。

参照用迭代法求非线性方程近似根的方法，解方程组的迭代法，首先需要将方程组（7.25）转化为一个等价方程组

然后从任意初始向量x（0）出发，按下述逐次代入方法构造向量序列｛x（k）｝：

解　方程组的精确解为x∗＝（2，－2，1）T。

首先将Ax ＝b 转化为等价方程组

迭代公式：任给初始向量，例如取x（0）＝（1，－1，1）T

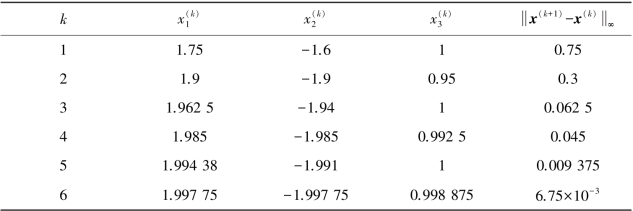
部分计算结果如表7.1 所示。(www.xing528.com)

表7.1　计算结果

且有误差

从此例可看出，由迭代法产生的向量序列｛x（k）｝逐次逼近方程组的精确解。 需要指出的是，方程组（7.25）转化为等价方程组（7.26）的形式并非唯一，这将影响到迭代过程的收敛性。不失一般性，在以下的讨论中，我们均假设方程组（7.25）中系数矩阵A 是非奇异的，且主对角元素aii≠0（i＝1，…，n）。

现将A 分裂为A＝M－N，于是方程组（7.25）等价于方程组

其中，M 为可选择的一个非奇异矩阵，并应选择M 使Mx ＝f 容易求解。 我们称M 为分裂矩阵。

对应于方程组（7.28），可构造一个迭代过程

其中，迭代矩阵B＝M－1N ＝M－1（M－A）＝I－M－1A。 选取不同的M 矩阵，就得到解Ax ＝b 的各种迭代法。