向量和矩阵范数：数值计算方法第3版成果

为了对方程组的计算解进行误差分析，以及讨论迭代法的收敛性，需要对Rn 中向量及Rn×n中矩阵引进某种度量，即引进向量或矩阵的范数概念。 Rn 中向量范数是R3 中向量长度概念的推广。

定义7.1　（向量范数）　如果向量x∈Rn 的某个实值函数N（x）≡‖x‖满足条件

①非负性：‖x‖≥0，且‖x‖＝0⇔x ＝0；

②齐次性：‖αx‖＝｜α｜‖x‖，α 为实数或复数；

③三角不等式：‖x＋y‖≤‖x‖＋‖y‖，对任意向量x，y∈Rn。

称N（x）≡‖x‖是Rn 上的一个向量范数（或向量的模）。

下面我们给出几种常用的向量范数。

定义7.2　设x ＝（x1，x2，…，xn）T∈Rn，定义Rn 上3 种常用的向量范数

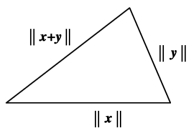
图7.1

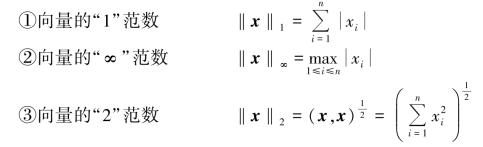
容易验证，上述定义的向量x∈Rn 的函数N（x）≡‖x‖υ（υ＝1，或∞或2）满足定义7.1 的3 个条件，因此，N（x）是Rn 上向量的范数。

例7.7　设x ＝（－1，2，3）T，计算‖x‖1，‖x‖∞，‖x‖2。

定义7.3　（向量序列的极限）

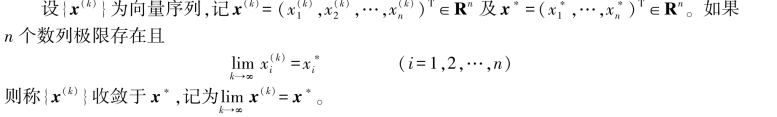
定理7.7　设N（x）＝‖x‖是Rn 上任一向量范数，则N（x）是x 的分量x1，x2，…，xn 的连续函数。

定理7.8　设‖x‖s，‖x‖t 是Rn 上向量的任意两种范数，则存在常数c1，c2＞0，使得对一切x∈Rn 有

证明可见参考文献［1］。

注：该定理说明，如果在一种范数意义下向量序列收敛时，则在任何一种范数意义下该向量序列均收敛。

定理7.9　设｛x（k）｝是Rn 中一向量序列，且x∗∈Rn，则

证　只就υ＝∞证明。

显然有

定义7.4　（矩阵的范数）(www.xing528.com)

如果矩阵A∈Rn×n的某个非负实值函数N（A）≡‖A‖满足下述条件：

①正定性：‖A‖≥0，且‖A‖＝0⇔A＝0；

③三角不等式：‖A＋B‖≤‖A‖＋‖B‖，对任意矩阵A，B∈Rn×n；

④相容性：‖AB‖≤‖A‖‖B‖。

则称N（A）≡‖A‖是Rn×n上一个矩阵范数（或模）。

在大多数与估计有关的问题中，会同时用到矩阵和向量。 下面借助于向量范数来定义矩阵范数。

定义7.5　（矩阵的算子范数）

设x∈Rn，A∈Rn×n，且给出一种向量范数‖x‖υ，相应的定义一个矩阵的非负函数N（A）＝‖A‖υ。 即

显然，由式（7.23）对任意x∈Rn，A∈Rn×n有

且容易验证N（A）＝‖A‖υ 满足矩阵范数条件①—④，所以‖A‖υ 是Rn×n上矩阵的范数，下面验证条件③和④成立。 事实上，利用向量范数的三角不等式及式（7.24）有

设x≠0，故有

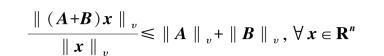
于是

同理，由式（7.24）有

‖ABx‖υ≤‖A‖υ‖Bx‖υ≤‖A‖υ‖B‖υ‖x‖υ。

当x≠0 时，有

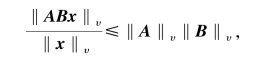
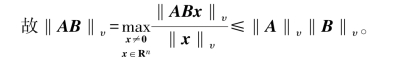
下面给出当υ＝1，∞，2 时，相应的矩阵算子范数‖A‖υ 的计算公式。

定理7.10　（矩阵范数计算公式）

设x∈Rn，A∈Rn×n，则