牛顿法公式及误差分析|数值计算方法

设有非线性方程

其中，假设f（x）在［a，b］上一阶连续可微，且f（a）·f（b）＜0；又设x0 是f（x）的一个零点x∗∈（a，b）的近似值（设f′（x0）≠0）。 现考虑用过曲线y ＝f（x）上点P（x0， f（x0））的切线近似代替函数f（x），即用线性函数

代替f（x）。 且用切线的零点x1 作为方程（6.13）的根x∗的近似值，即

一般地，若已求得xk，将式（6.16）中x0 换为xk，重复上述过程，即得求方程f（x）＝0 根的牛顿法的计算公式

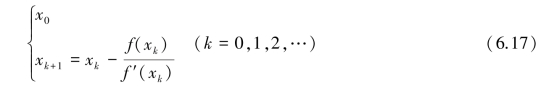
在几何上，线性化方程f（xk）＋f′（xk）（x－xk）＝0 的解xk＋1，表示过曲线y ＝f（x）上点P0（xk，yk）的切线与x 轴的交点，如图6.2 所示。

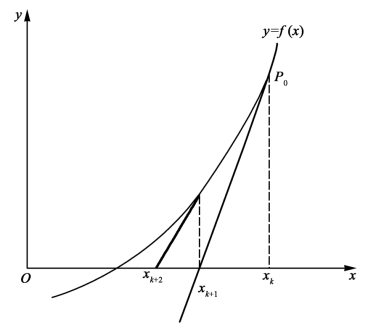
图6.2　牛顿法的几何意 义(www.xing528.com)

下面利用f（x）的泰勒公式进行误差分析。 设已知f（x）＝0 的根x∗的第k 次近似xk，于是f（x）在xk 点泰勒公式为（设f（x）二次连续可微）：

利用牛顿法公式（6.17）即得误差关系式

误差公式（6.19）说明xk＋1的误差是与xk 的误差的平方成比例的。 当初始误差充分小时，以后迭代的误差将非常快地减少。

计算结果见表6.5。

表6.5　计算结果

注：当初值x0 选取靠近根x∗时，牛顿法收敛且收敛较快；当初值x0 不是选取接近方程根时，牛顿法可能会给出发散的结果。