![]()

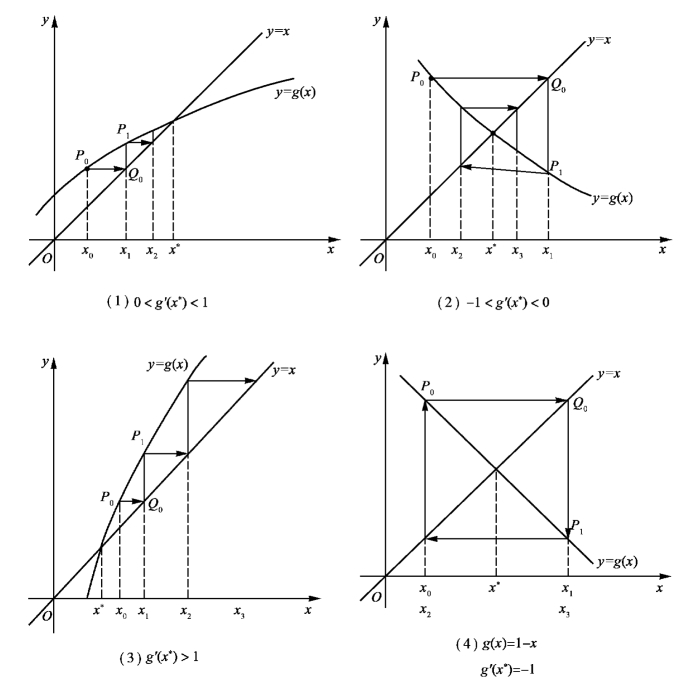
图6.1 迭代法的几何意义
定理6.1 设g(x)在[a,b]上连续,且满足
①当x∈[a,b]时,有g(x)∈[a,b];
②存在常数L∈(0,1),使得对任意x,y∈[a,b]都有
![]()
则g(x)在[a,b]上有唯一的不动点x∗。
证 先证明不动点的存在性。 若g(a)=a 或g(b)=b,显然g(x)在[a,b]上存在不动点。由条件①,以下设g(a)>a 及g(b)<b,定义函数f(x)=g(x)-x。 显然f(x)∈C[a,b],且f(a) f(b)<0,由零点存在定理可知存在x∗∈(a,b)使f(x∗)=0,即x∗=g(x∗),x∗即为g(x)的不动点。

故g(x)的不动点是唯一的。
在g(x)的不动点是唯一的情况下,可得到迭代法收敛的一个充分条件。

![]()
证 由定理6.1 的条件①,当x0∈[a,b]时,有xk∈[a,b],k =1,2,…。 设x∗是g(x)在[a,b]上的唯一不动点,则由条件②得
![]()
![]()
下面证明误差估计式(6.7)。 由迭代公式xk+1 =g(xk),显然有
![]()
反复利用式(6.8)式递推得|xk+1-xk |≤Lk |x1-x0 |。
于是
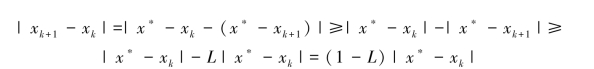
即
![]()

②当g(x)在[a,b]上具有连续导数时,定理中的条件②可用
![]() (https://www.xing528.com)
(https://www.xing528.com)
代替。
上面给出了迭代序列{xk}在区间[a,b]上的收敛性,通常称为全局收敛性。 对定理中的假设条件:当x∈[a,b]时,|g′(x)|≤L<1。 在一般情况下,可能对于大范围的含根区间不满足,而在根的邻域内是成立的,为此有下述迭代过程局部收敛性结果。
定理6.3 (迭代法的局部收敛性) 给定方程x =g(x),设
①x∗为方程的解;
②g(x)在x∗的邻近连续可导且有|g′(x∗)|<1
则对任意取初值x0∈S =[x∗-δ,x∗+δ],δ>0,迭代过程xk+1 =g(xk)(k =0,1,2,…)收敛于x∗(此时称迭代过程具有局部收敛性)。
证 取[a,b]=[x∗-δ,x∗+δ],于是只要验证定理6.2 中条件②成立即可。
事实上,设x∈S,则x1 =g(x)满足
![]()
![]()
这说明x1 =g(x)∈S。
例6.4 试用迭代法解方程: f(x)=x-ln(x+2)=0。
解 ①由于当x>-2 时, f(x)连续,且显然有
![]()
![]()
②考察取初值x0∈[0,2]时,迭代过程xk+1 =ln(xk +2)的收敛性,其中迭代函数为g1(x)=ln(x+2)。

于是由定理6.3 可知,当初值x0∈[0,2]时迭代过程xk+1 =ln(xk+2)收敛,结果见表6.3。
表6.3 计算结果


④可将方程转化为等价方程ex =x+2,从而x =ex-2≡g2(x),且有g′2(x)=ex。
因为当x∈[-1.9,-1]时,|g′2(x)|≤g′2(-1)≈0.368<1,所以,当选取初值x0∈[-1.9,-1]时,迭代过程
![]()
![]()
由上例可见,对于方程f(x)=0,迭代函数g(x)选取不同,相应由迭代法产生的{xk}收敛情况也不一样。 因此,我们应该选择迭代函数,使构造的迭代过程xk+1 =g(xk)收敛且较快。 对于收敛的迭代过程,只要迭代足够多次,就可以使结果达到任意的精度,但有时迭代过程收敛缓慢,从而使计算量变得很大,因此迭代过程的加速是个重要的课题。 相关的加速方法可参看文献[1]。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




