【摘要】：，an，使达到最小。，an 的线性方程组：方程组（3.3）称为法方程组。可以证明，该方程组有唯一解例3.1已知某单位2001—2007 年的利润为试预测2008 年的利润。计算得图3.1散点图从而得方程组解得于是将t＝8 代入，得2008 年的利润为例3.2求数据：的最小二乘二次拟合多项式。解依题意，设二次拟合多项式为p2＝a0＋a1x＋a2x2，将数据代入得线性方程组解得所以最小二乘二次拟合多项式为
设已知点（xi，yi）（i＝1，2，…，m），求n 次多项式Pn（x）来拟合函数f（x）。设Pn（x）＝a0＋a1x＋…＋anxn，求系数a0，a1，…，an，使
达到最小。
当拟合函数是一元函数时，所对应的函数图形是平面曲线。 这时，数据拟合问题的几何背景是寻求一条近似通过给定离散点的曲线，故称为曲线拟合问题。
由于函数F（a0，a1，…，am）达到最小，所以由高等数学知识有
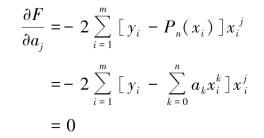
即
于是得到关于a0，a1，…，an 的线性方程组：
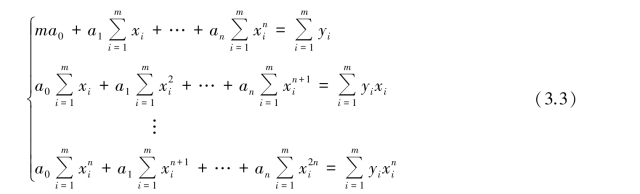
方程组（3.3）称为法方程组。 可以证明，该方程组有唯一解
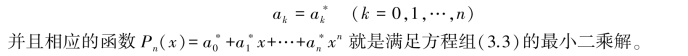
例3.1 已知某单位2001—2007 年的利润为
试预测2008 年的利润。
解 由已知数据作出散点图（如图3.1），可见该单位的年利润几乎直线上升。 选择一次多项式作为拟合函数来预测2008 年的利润。 为简化计算，将年份记为xi ＝2 000＋ti，相应年份的利润记作yi，则所求的拟合函数为y ＝a＋bt。 计算得
图3.1 散点图
(www.xing528.com)
从而得方程组
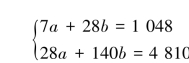
解得
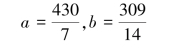
于是
将t＝8 代入，得2008 年的利润为
例3.2 求数据：
的最小二乘二次拟合多项式。
解 依题意，设二次拟合多项式为p2（x）＝a0＋a1x＋a2x2，将数据代入得线性方程组
解得
所以最小二乘二次拟合多项式为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
