三次样条插值方法数值计算方法

代数插值多项式有很好的光滑性，但随节点增加反而精度降低，因为高阶差分误差传播大。 分段低次插值算法简单，近似程度好，然而光滑性差。 由于航空、造船等高精端工程设计的需要而发展起来的样条插值方法，既保留了分段低次插值的各种优点，又提高了插值函数的光滑性，在许多领域都有广泛的应用。

样条插值是用样条函数去逼近函数。

定义2.4　对区间［a，b］的一个划分Δ：a ＝x0＜x1＜…＜xn－1＜xn ＝b，函数S（x）满足：

1）S（x）在［xi，xi＋1］，（i＝0，1，…，n－1）上为k 次多项式；

2）S（x）及其1，2，…，k－1 阶导数在区间［a，b］连续。

则称S（x）为区间［a，b］上对应于划分Δ 的k 次多项式样条函数，x0，x1，…，xn 为样条节点。 且若对于节点xi 上给定的函数值f（xi）＝yi（i＝0，1，…，n），有

则称S（x）为k 次样条插值函数。

k ＝1 时的样条插值函数就是分段线性插值，k ＝3 时是使用较多的三次样条插值函数。

例2.10　已知函数

是以0，1，2 为节点的三次样条函数，求系数b，c 的值。

解　取x0 ＝0，x1 ＝1，x2 ＝2，由定义知S（x）∈C2［0，2］，即

于是由S（x）和S′（x）分别在x1 ＝1 处连续得

解得b ＝－ 2，c ＝3

为求解三次样条插值函数，先介绍三次样条插值问题。 设

其中Si（x）（i＝1，…，n）为不超过三次的多项式。

三次样条插值函数S（x）在每个子区间［xi，xi＋1］上可用三次多项式的4 个系数唯一确定，因此S（x）在［a，b］上有4n 个待定参数。

由于S（x）∈C2［a，b］，有

该条件给出了3（n－1）个约束。 另外，插值条件

给出了n＋1 个约束。 从而总共给出了4n－2 个约束，与待定参数相比还少2 个约束。 为了确定S（x），在区间［a，b］的端点处补充两个条件，称为边界条件。 常用的边界条件有下列3 种。

①给定端点的一阶导数值S′（x0）＝y′0，S′（xn）＝y′n；

②给定端点的二阶导数值S″（x0）＝y″0，S″（xn）＝y″n；特别地，对于S″（x0）＝S″（xn）＝0 的边界条件称为自然边界条件；

③周期边界条件S（x0）＝S（xn），S′（x0）＝S′（xn），S″（x0）＝S″（xn）。

下面仅介绍三次样条插值函数的具体构造方法。

（1）用节点处一阶导数表示三次样条插值函数

记S′（xj）＝mj（j＝0，1，…，n），则在区间［xj，xj＋1］（j＝0，1，…，n－1）上满足：

设hj ＝xj＋1－xj，当x∈［xj，xj＋1］时，有

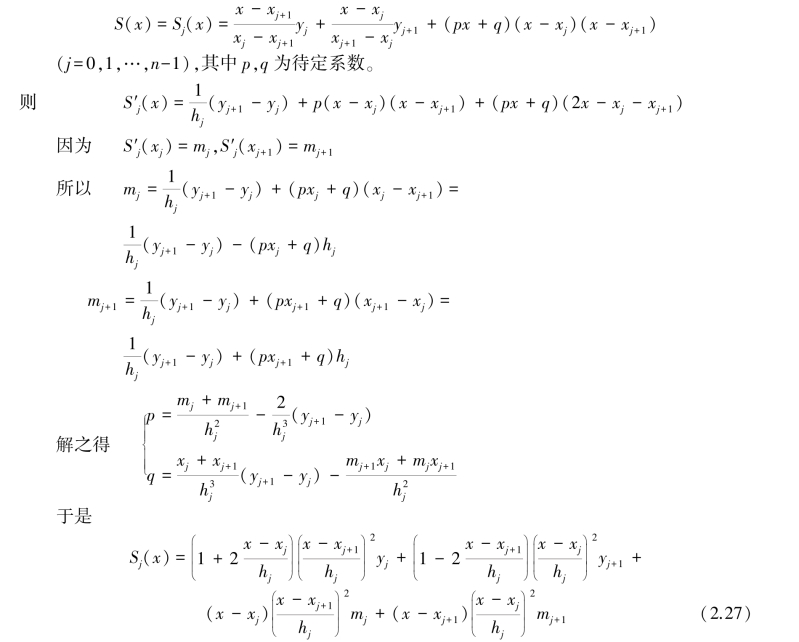
由二阶导数在内节点处连续S″j（xj＋0）＝S″j－1（xj－0），　j＝1，2，…，n－1可导出关于参数mj 的方程组

其中

注：方程组中参数m0 ＝y′0，mn ＝y′n已知时，称式（2.28）为三转角方程。

（2）用节点处二阶导数表示三次样条插值函数

令S″（xi）＝y″i ＝Mi，i＝0，1，…，n。

当x∈［xj，xj＋1］时，直线S″（x）＝S″j（x）过（xj，Mj）和（xj＋1，Mj＋1）两点，从而有

对上式连续积分两次

根据插值条件Sj（xj）＝yj，Sj（xj＋1）＝yj＋1确定出任意常数c1j，c2j，

(www.xing528.com)

于是

由上式知，只要求出所有的参数Mj，就可确定Sj（x）。

对上式求导，并利用一阶导数的连续性：S′j－1（xj－0）＝S′j（xj＋0），j＝1，…，n－1 得

或

则可得方程组

其中

方程组（2.31）称为三弯矩方程。 它含有n＋1 个参数M0，M1，…，Mn，还需要利用前面的任一组边界条件才能完全确定所有参数。 例如，给定边界条件

由式（2.30）可分别得方程

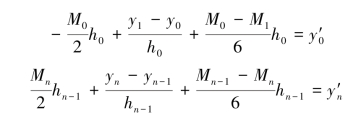
即

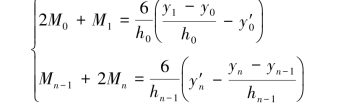
注：若是第二种边界条件，则M0，Mn 是已知的。

例2.11　已知函数在节点处函数值

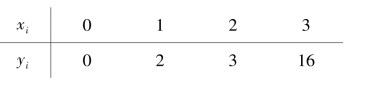
求满足边界条件y′（0）＝1，y′（3）＝0 的三次样条插值函数。

解　方法1　用一阶导数为参数的三转角方程

因为m0 ＝1，m3 ＝0，所以得三转角方程

方法2　用二阶导数为参数的三弯矩方程

由边界条件得

于是得三弯矩方程

或用矩阵形式表示为

则三次样条插值函数为

注：本题是第1 种边界条件，用三弯矩方程求解要复杂一些。

例2.12　已知数据表

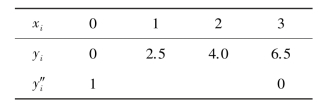
求y ＝f（x）在［0，3］上的三次样条插值函数，并作图。

将M0 ＝1，M3 ＝0 代入得

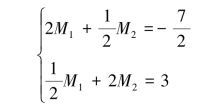
图形如图2.3 所示：

图2.3　三次样条插值函数