【摘要】：由插值问题的定义可知，多项式插值问题是：在区间［a，b］上，根据函数表（2.1），构造一个次数不超过n 的代数多项式pn＝a0＋a1x＋a2x2＋…事实上，由条件（2.3）知，插值多项式pn的系数满足线性方程组所以该方程组有唯一解，即插值多项式存在且唯一。插值多项式pn与f的插值余项Rn＝f－pn满足下面的余项定理。
求f（x）的插值多项式p（x）的几何意义，就是通过曲线y ＝f（x）上的若干个插值节点，作一条代数多项式曲线y ＝p（x）来近似代替曲线y ＝f（x）（如图2.1 所示）。
由插值问题的定义可知，多项式插值问题是：在区间［a，b］上，根据函数表（2.1），构造一个次数不超过n 的代数多项式pn（x）＝a0＋a1x＋a2x2＋…＋anxn，使
而在其余点x 处，一般说来会有误差，这个误差称为插值多项式的插值余项或截断误差，记为Rn（x），即
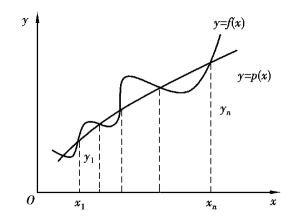
图2.1 插值法的几何意义
下面是关于插值多项式的基本定理。
定理2.1 满足插值条件（2.3）的n 次插值多项式是存在且唯一的。
事实上，由条件（2.3）知，插值多项式pn（x）的系数满足线性方程组
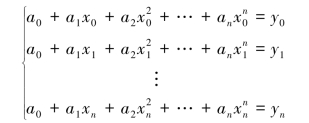(https://www.xing528.com)
所以该方程组有唯一解，即插值多项式存在且唯一。
注：对于次数不大于n 的多项式f（x），其n 次插值多项式就是其本身。
插值多项式pn（x）与f（x）的插值余项Rn（x）＝f（x）－pn（x）满足下面的余项定理。
定理2.2（误差估计） 设f （n）（x）∈C［a，b］，任意x∈（a，b），f （n＋1）（x）存在，x0，x1，x2，…，xn 为n＋1 个互异插值节点，pn（x）为f（x）在［a，b］上的n 次插值多项式，则对任意x∈［a，b］有余项
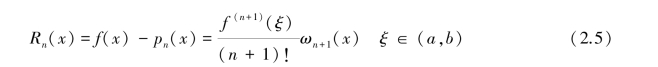
其中
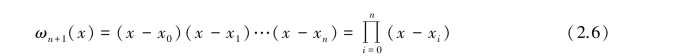
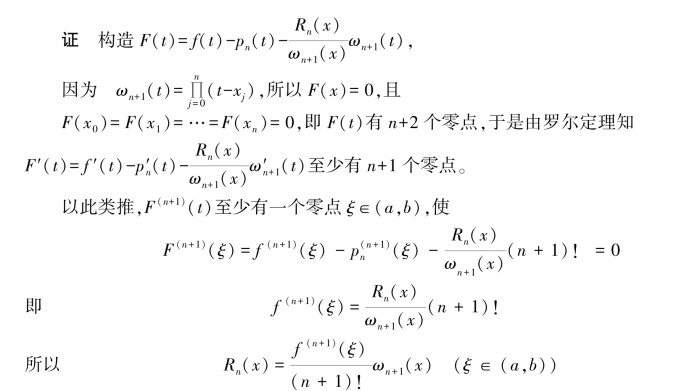
注意：这里ξ∈（a，b）且依赖于x。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
