数值计算方法算法数值稳定性

通过前面对误差传播规律的分析，同一问题当选用不同的算法时，它们所得到的结果有时会相差很大，这是因为运算中的舍入误差在运算过程中的传播常随算法而异。 凡一种算法的计算结果受舍入误差的影响小者称它为数值稳定的算法。 下面举几个例子来说明。

例1.7　解方程　

解　由韦达定理可知，此方程的精确解为

如果利用求根公式

来编制计算机程序，在字长为8、基底为10 的计算机上进行运算，则由于计算机实际上采用的是规格化浮点数的运算，这时

的第二项中最后两位数“01”，由于计算机字长的限制，在机器上表示不出来，故在计算机对阶舍入运算时为

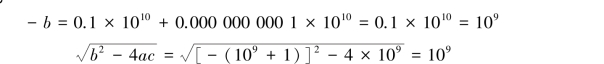
于是

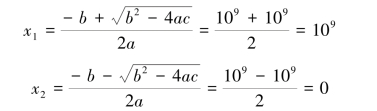
所得结果很好。 这说明第二种算法有较好的数值稳定性。

注：在利用根与系数关系式求第二根时，必须先算出绝对值较大的一个根，然后再求另一个根，才能得到精度较高的结果。

例1.8　试计算积分

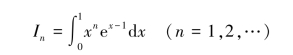
解　由分部积分法可得

因此，有递推公式In ＝1 － nIn－1（n ＝1，2，…），其中I1 ＝1／e。

用上面的递推公式，在字长为6，基底为10 的计算机上，从I1 出发计算前几个积分值，其结果如表1.1。

表1.1　计算结果

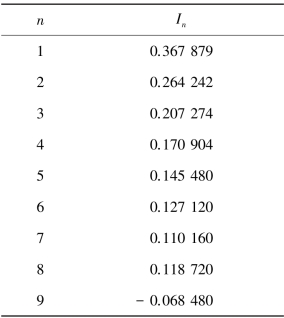
被积函数xnex－1 在积分限（0，1）区间内都是正值，积分值I9 取三位有效数字时的精确结果为0.091 6，但上表中的I9 ＝－ 0.068 480 却是负值，与0.091 6 相差很大。 怎么会出现这种现象？ 可分析如下。(www.xing528.com)

由于在计算I1 时有舍入误差约为ε ＝4.412 × 10－7，且考虑以后的计算都不再另有舍入误差。 此ε 对后面各项计算的影响为

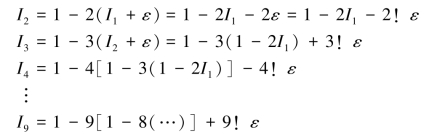
这样，算到I9 时产生的误差为9！ ε ≈0.610 1 就是一个不小的数值了。

可以改进算法来提高此例的数值稳定性，即将递推公式改写为

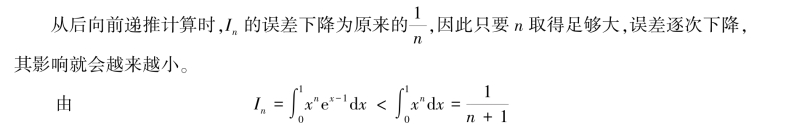
可知：当n→∞时In→0。 因此可取I20 ＝0 作为初始值进行递推计算。

到计算I15时，误差已下降到10－8以下，结果如表1.2。

表1.2　计算结果

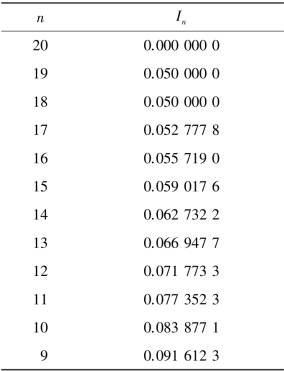
这样得到的I9 ＝0.091 612 3 已很精确了。 可见经过改进后的新算法具有很好的稳定性。

例1.9　对于小的x 值，计算ex－1。

解 如果用ex－1 直接进行计算，其稳定性是很差的，因为两个相近数相减会严重丢失有效数字，产生很大的误差。 因此得采用合适的算法来保证计算的数值稳定性。 可以把ex 在点x ＝0附近展开成幂级数：

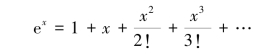
则可得

按上式计算就有很好的数值稳定性。

通过以上这些例子，可以知道算法的数值稳定性对于数值计算的重要性了。 如无足够的稳定性，将会导致计算的最终失败。 为了防止误差传播、积累带来的危害，提高计算的稳定性，将前面分析所得的各种结果归纳起来，得到数值计算中应注意如下几点：

①应选用数值稳定的计算方法，避开不稳定的算式。②注意简化计算步骤及公式，减少误差的积累；设法减少乘除法运算，节约计算机的机时。例如前面讲到过的用秦九韶算法计算多项式，就是一个改变计算公式以减少运算次数的极好例子。

③应合理安排运算顺序，防止参与运算的数在数量级相差悬殊时，大数“淹没”小数的现象发生。

④应避免两相近数相减，可用变换公式的方法来解决。

⑤绝对值太小的数不宜作为除数，否则产生的误差过大，甚至会在计算机中造成“溢出”错误。