ADINA有限元-阶段求解增强案例

计算是否易于收敛与初始条件相关，当给定的初始条件与最终结果相差较大时，计算将很难收敛，此时应该考虑增加几个求解阶段来加强收敛。

例如，对于如图7-27所示的强迫对流问题进行稳态分析，底部的边界将受热。进口处指定的流速迫使流体在整个空腔内流动，底边受热主要通过对流传递。如果施加图中的边界条件，模型将不能够收敛。

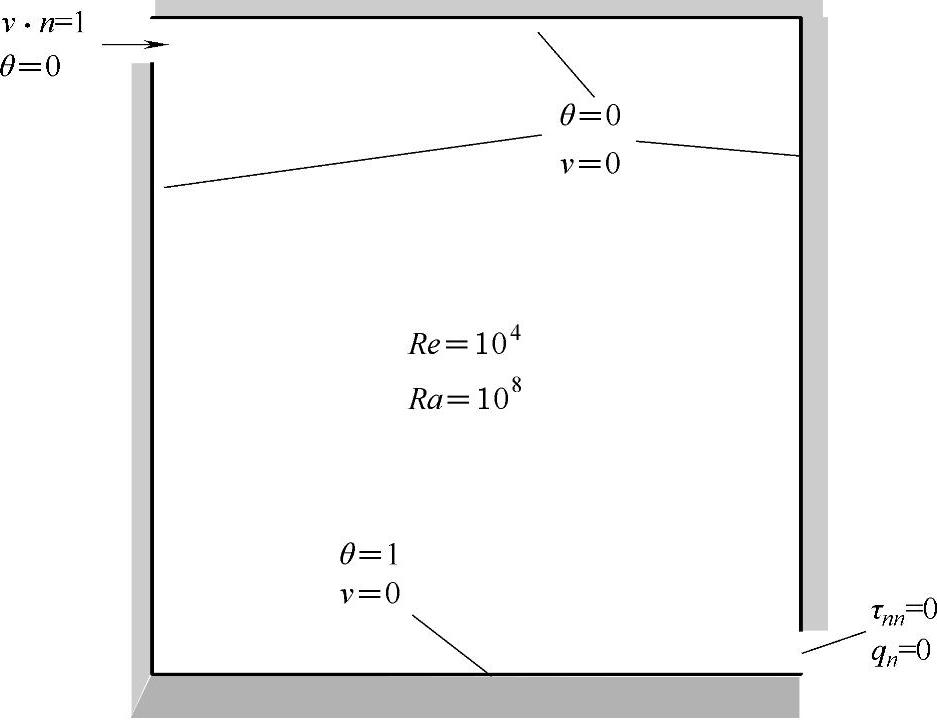
图7-27 强迫对流问题示意图

此时，可以通过两个计算阶段来求解上述问题：1）进行不考虑传热的流体计算；2）进行考虑流体流动的传热计算。在每个单独的计算阶段，都比较容易收敛。

第1阶段，如图7-28所示。为了使计算更容易收敛，还可以分两个时间步进行：第1个时间步中指定相对较小的速度，且施加雷诺数为1000的边界条件，这样即使在没有初始条件的情况下也容易采用牛顿迭代法进行求解；第2个时间步将以第1个时间步的计算结果作为初始条件，并施加全速度，将雷诺数设置为10000，此时并未考虑底部的温度载荷，即瑞利数为0。

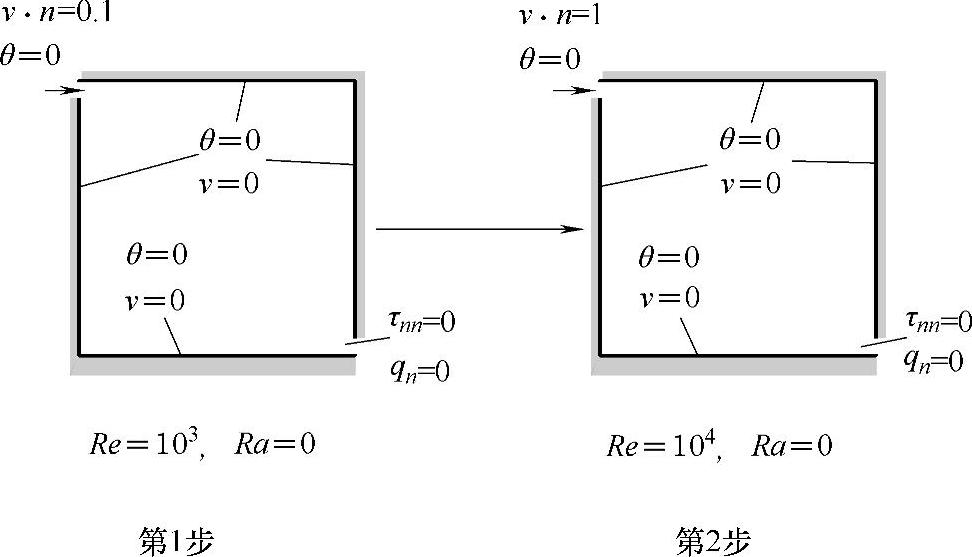
图7-28 第1阶段强迫对流计算(www.xing528.com)

第2阶段（见图7-29）则保持流体边界条件不变而让底面逐渐升温，该阶段可在2～6个时间步中完成：首先，可以在第1个阶段的计算结果上定义比较小的瑞利数（例如，10000）来作为第2个阶段第1个时间步的初始条件，这样做将有助于计算收敛；此后，每个时间步的计算结果都将自动作为下一时间步的初始条件。该示例的时间步长可以按表7-1进行设定。

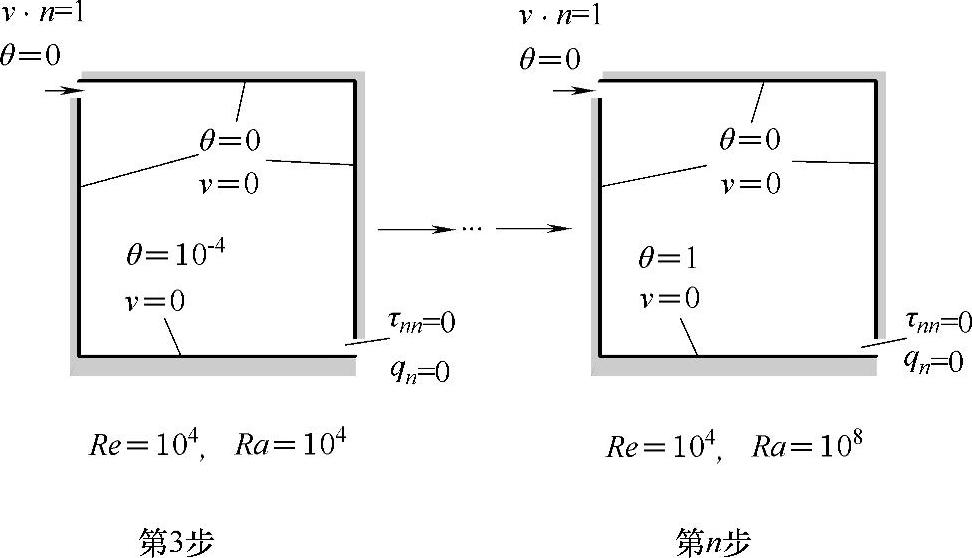
图7-29 第2阶段强迫对流计算

表7-1 时间步长的设定

需要注意的是：此时进行的是稳态计算，每个时间步的计算结果是对应时间下的稳态解，时间仅是一个控制边界或载荷的参数，没有任何物理意义。