【摘要】：稳态分析中的时间步没有任何物理意义，定义时间函数的目的是用来确定各时间步下的载荷情况。瞬态分析中的时间步则有物理意义，因此，计算时间步长的大小必须设置合理。对于微可压缩流体，波速w的表达式为：式中，，是流场体积模量；p是压力；ρ是密度。对于可压缩流体，波速与音速相同，表达式为：式中，c是声速；γ≡cp/cV，是比定压热容与比定容热容的比值。图7-10 波动问题中时间步长的选取
稳态分析中的时间步没有任何物理意义，定义时间函数的目的是用来确定各时间步下的载荷情况。瞬态分析中的时间步则有物理意义，因此，计算时间步长的大小必须设置合理。对于隐式方法，时间步长的大小没有任何限制，只需方程能够迭代收敛即可，因此，时间步长的选取只与感兴趣的实际物理条件有关。
许多瞬态问题都有时间周期性，一般情况下，该类问题最小的合理时间步长应取为时间周期的1/100～1/20，如图7-9所示。
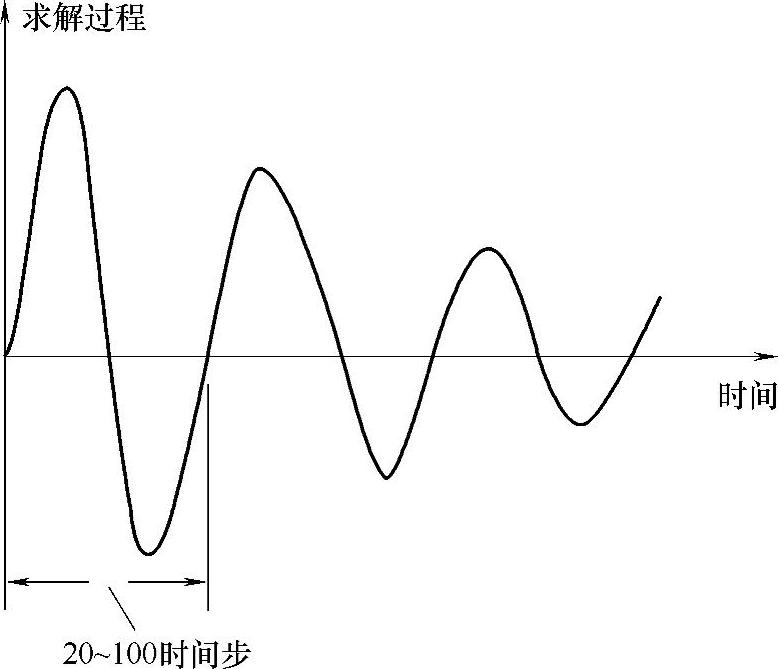
图7-9 周期性瞬态问题中时间步长的选取
某些瞬态问题的时间步长则完全由所关心区域的波动情况决定，即：时间步长必须小到足以捕捉到波的运动过程。
对于微可压缩流体，波速w的表达式为：
式中，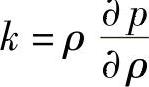
，是流场体积模量；p是压力；ρ是密度。(www.xing528.com)
对于可压缩流体，波速与音速相同，表达式为：
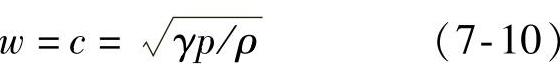
式中，c是声速；γ≡cp/cV，是比定压热容与比定容热容的比值。
一般情况下，如果10倍时间步长下波动的最小距离为L，则L/10w就是允许的最大时间步长。从另一方面来看，如果时间步长太小将造成计算时间步太多，往往也没有必要。L/10w是时间步长的上限值，Δx/w则是时间步长的下限值（如图7-10所示），其中，Δx指的是单元尺寸。
对于比较复杂的问题，为了捕捉到模型在整个时间过程的响应，时间步长应该尽量取小值。当步长足够小时（CFL值大约为1），则可以忽略计算的平衡迭代。尤其对于包含很多时间步的计算问题，忽略平衡迭代可以节省大量的CPU时间，一般可以达到50%～90%。
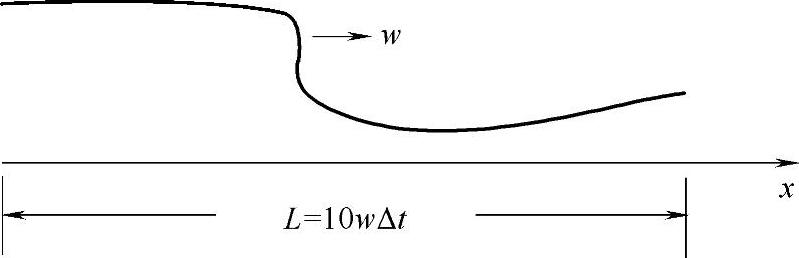
图7-10 波动问题中时间步长的选取
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
