ADINA有限元分析的经典实例

模拟稳态流动问题时，既可以选用稳态分析类型，也可以选用瞬态分析类型。稳态流动问题所有的材料和边界条件都与时间无关。ADINA-CFD模块中定义稳态流动的主要目的是为了消除控制方程内的动力项∂（）/∂t。

通过下列五种方法可以获得稳态分析的结果：

1）进行只包含一个时间步的稳态分析。其中，材料和边界都与时间无关，该方法比较适用于某些简单的流体问题。

2）在方法1中使用适当的CFL值（请参见本节末尾处的介绍）。就数值稳定性而言，CFL选项与瞬态分析的时间推进相同，它们都可以得到稳态的分析结果。此外，采用CFL选项的优点在于：ADINA软件能够自动选择时间步长，且计算结果是稳态解，该方法适用于所有的流体问题。尤其需要注意的是：如果选用的CFL值非常大，则与方法1的作用相同。选用适当的CFL值可以极大地改善计算的收敛性，CFL的取值不能太小，对于隐式方法，其下限值为1。

3）进行多个时间步的稳态分析，材料或边界都可以与时间相关。此时，时间步并非指的是真实时间，将其看做是载荷步更合适。每个时间步的计算结果都是对应时间条件下的稳态结果，前一个时间步的计算结果可以作为下一个时间步计算的初始条件。该方法非常适用于包含过渡阶段的流体，例如，自然对流、弯管流动、流体循环流动等。计算过程中每个时间步可能采用不同的载荷条件，例如，不同的雷诺数、瑞利数等。虽然该方法需要更多的时间步，但由于比方法1中的初始条件更接近实际情况，因此其收敛性要比方法1更强。

4）在方法3中使用适当的CFL值。如果CFL取值合适，则方法4将比方法3的稳定性更好。虽然过小的CFL值会造成收敛缓慢，但该方法仍然是进行稳态分析的常用方法。

5）也可以通过瞬态分析来逼近稳态分析的结果。可以用将时间向前推进或必要的重启动方法来得到稳态结果。由于通常只关心最终的结果，因此可以忽略瞬态分析中间过程的平衡迭代，这时可以将计算的收敛容差调大或者将最大的迭代次数设置为1。稳态分析的收敛容差则按正常进行设置，以保证获得正常的结果。如果采用时间向前推进的方法仍然无法得到稳态结果，则可以通过查看最终的计算结果来判断是否已经达到稳态，或将其作为重启动的初始条件进行必要的重启动分析。

对于某些非稳态的流动问题，则必须采用瞬态的分析类型来处理。此时，初始条件必须是真实的物理条件，时间步也必须是有物理意义的真实时间。当时间步长比较大时，必须进行包含平衡迭代的收敛计算，以保证瞬态分析的准确性。

提示：由于截断误差是引起误差的主要原因，计算结果的精度将与时间步长有关，除非CFL的值非常小（例如，CFL值为1）。一般情况下，瞬态问题最好采用隐式动力平衡迭代计算。如果时问步长非常小，则可以通过设置一个大的收敛容差或将最大迭代次数设置为1来忽略平衡迭代，此时的操作流程与方法5）相同。

●CFL（Courant-Friedrichs-Lewy）

在ADINA-CFD模块中单击图标，在弹出的对话框中勾选Automatic Time Step选项，单击右侧的图标，将弹出如图7-7所示的对话框，其中的Courant Number即为CFL数。默认情况下，如果不使用CFL数，则该值为无穷大。对于大部分隐式计算，CFL数的设置区间为（10²～10⁷）。对于显式时间积分，CFL数通常设置为0.8～0.9。

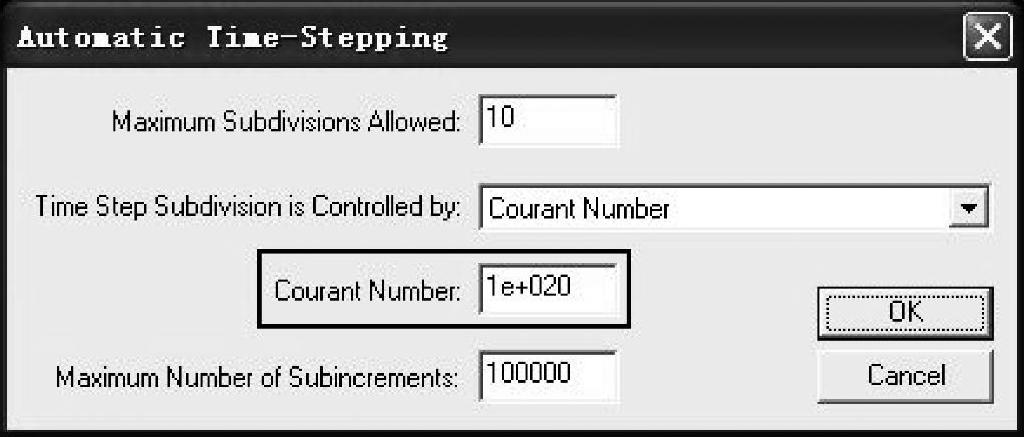
图7-7 设置CFL数

对于瞬态分析，合理的CFL数可以促进每个时间步的迭代收敛。对于稳态分析（时间为无穷大），收敛则意味着得到最终的收敛解，每一个平衡迭代就起到时间步的作用。(www.xing528.com)

一般情况下，CFL数越大则模型越不稳定、越不容易收敛；CFL数越小则模型越稳定，越容易收敛。但是，减小CFL数将导致收敛速度变慢。CFL数过小则使得迭代次数显著增加。对于隐式分析，CFL数的下限为1。合适的CFL数可以根据数值模拟和经验选取。使用适当的CFL数和控制每个时间步的载荷增量，可以解决很多涉及稳定性和收敛性的问题。关于CFL数的更详细介绍，请参见ADINA流体理论手册12.1节。

ADINA-CFD的稳态分析中不包含时间项，因此无需考虑时间项的积分。但是，瞬态分析中必须选择积分方法。ADINA软件中提供了两种时间积分方法：Euler积分和Composite积分，这两种积分方法都属于隐式积分算法。在ADINA-CFD模块中单击图标，在弹出的Transient Analysis对话框中单击Intergration Method右侧的下三角按钮，就可以选择不同的时间积分方法，默认选择为Euler（欧拉）积分，如图7-8所示。

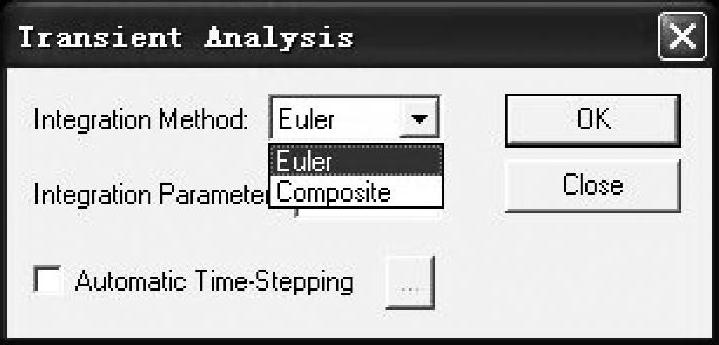
图7-8 设定时间积分方法

假设已经得到了t时刻的解，现在要求t+Δt时刻的解。其中，Δt表示时间步长，在t=0时刻初始条件定义。下面将介绍这两种积分算法：

Euler积分：方程∂u/∂t=f（u）根据式（7-6）进行计算：

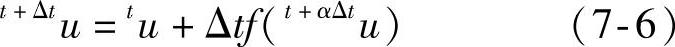
式中，。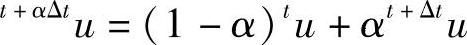

Euler积分属于一阶精度的算法，当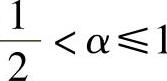时，计算结果是无条件稳定的。当α=1/2时，虽然在时间上能够达到二阶精度，但分析结果是不稳定的（除非速度非常小）。默认的一阶精度算法是欧拉向后积分方法（Euler Backward Method），此时α=1。

Composite（复合）积分：t+Δt时刻的解将根据式（7-7）和式（7-8）两个连续的子时间步进行计算：

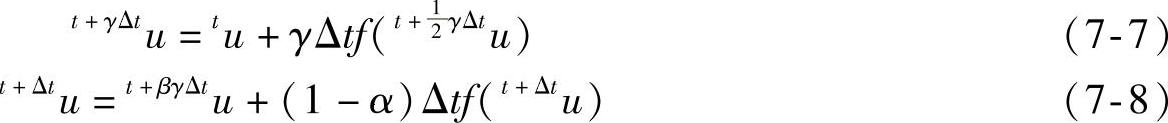
式中，；；。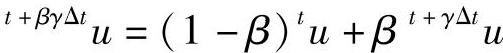

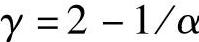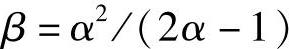当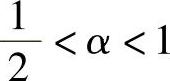时，该方法是二阶精度，且无条件稳定。α的默认值为1/2，此时截断误差将达到最小。与Euler积分相比，虽然每个时间步的计算代价加倍，但Composite积分方法得到的解更加精确，并且所需的时间步减少，占用CPU的时间也将减少。Composite积分方法最常用于计算瞬态脉动压力问题。例如，漩涡脱落、涡激流固耦合振动等。