基于任务完成时间的自适应算法：云计算任务优化调度技术研究

根据5.3.1建立的任务完成时间感知的调度模型，得到自适应的纳什均衡优化问题，其约束是资源依据任务的优先级及任务完成时间的公平性分配，以此基于梯度投影的方法，给出任务完成时间模型的调度优化GP算法，并考虑优先级设置的优化条件，优化目标定义：

其中，Ii为每个任务包含的线程数量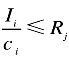，表示任务所获得的总资源必须能使得任务在规定的最晚完成时间前完成。

利用拉格朗日函数表示公式（5-32），如公式（5-33）所示：

其中，α、β为拉格朗日因子。

考虑应用梯度投影方法求得优化问题BR的解，梯度投影函数S表示如公式（5-34）所示，递归步长为，L是拉格朗日约束：

定义5.4令为BR的优化解，定义递归过程：

其中，r是R的梯度投影因子。

定义5.5对于递归过程｛r（k+1）｝，如果收敛，则有：(www.xing528.com)

因此，求得优化问题BR的解。

考虑资源分配的公平性，保证不同类型最晚完成时间的任务要求，根据以上对于优化问题的求解，资源分配GP算法描述：

步骤1：初始化任务的基本资源需求量Di、递归步长Δ"∈（0，L/2］系统资源量序列｛R1，R2，…，Rj，…，Rm｝；

步骤2：计算待分配资源的任务集中分配的投影梯度S（k）；

步骤3：判断梯度投影S（k）与用户提供的梯度投影允许误差值的关系，如果，且Δ"＜L/2，则转到步骤4，否则转到步骤2；

步骤4：更新S（k）；

步骤5：求得R'，结束算法。