(1)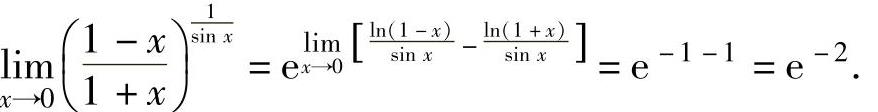
(2)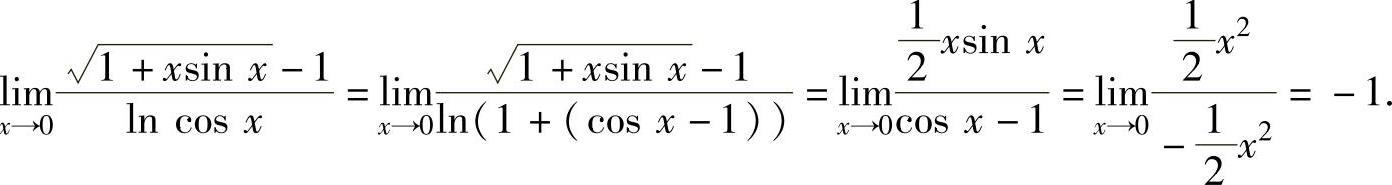
(3)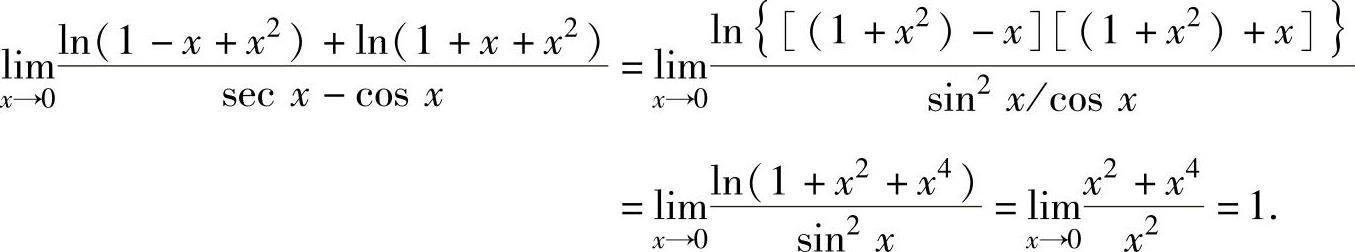
(4)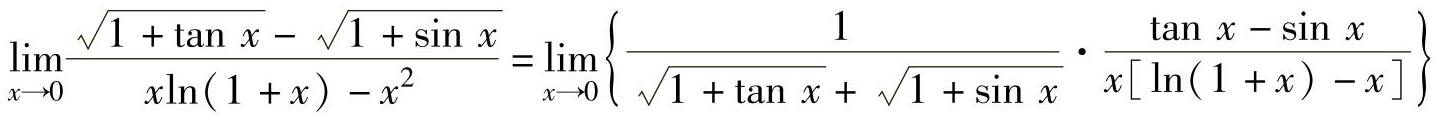
(5)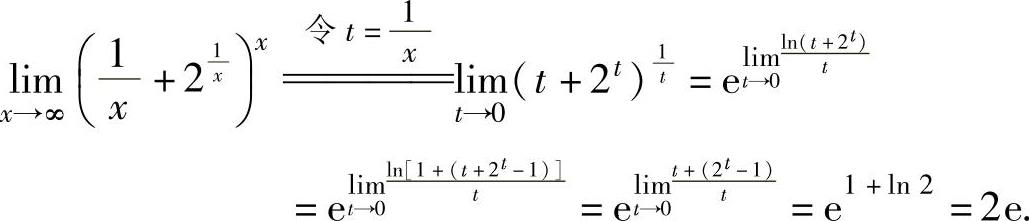
(6)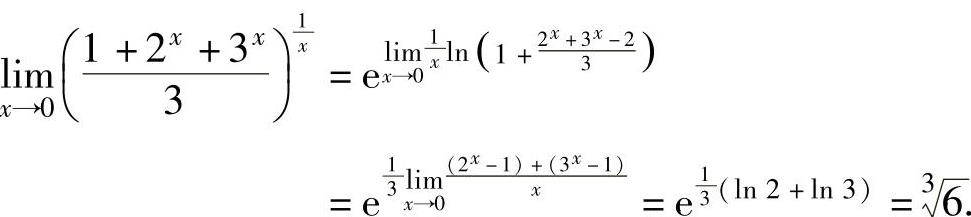
(7)由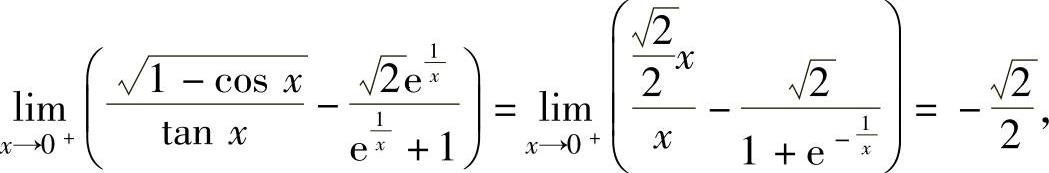
得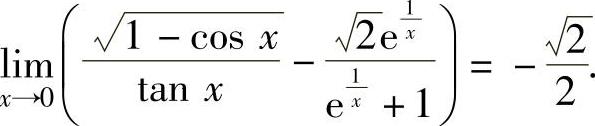
(8)由于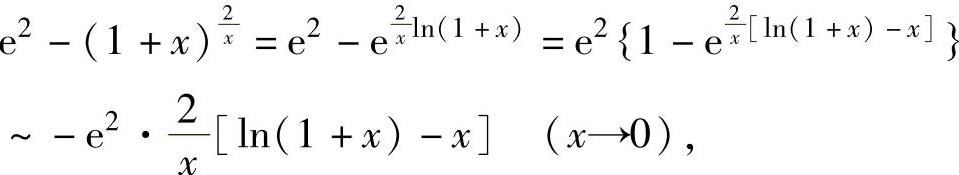
所以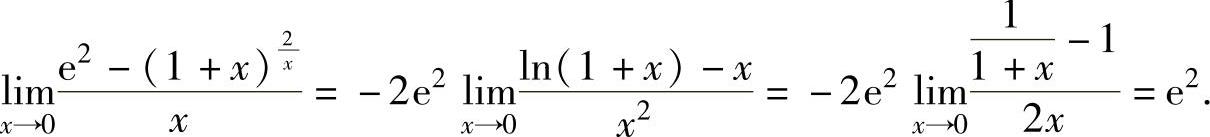
(9)由于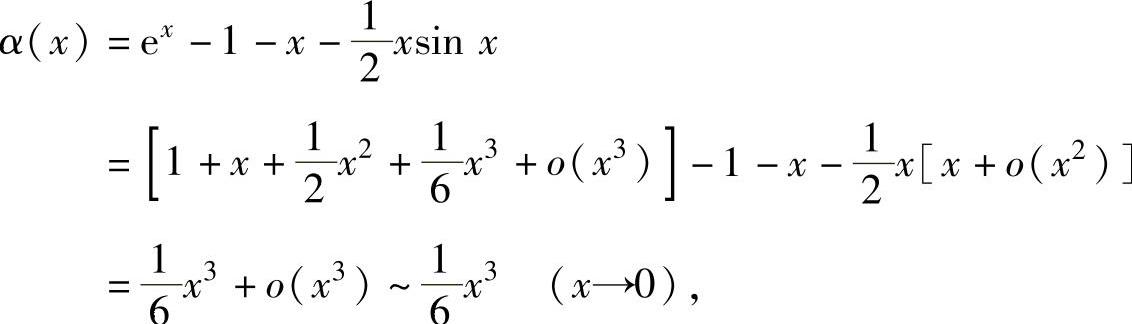
所以,x→0时,α(x)是x的三阶无穷小.
(10)记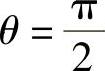 ,则
,则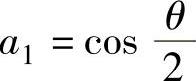 ,
,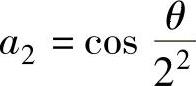 ,…,
,…,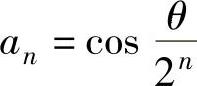 ,从而
,从而
(11)
(12)由题设知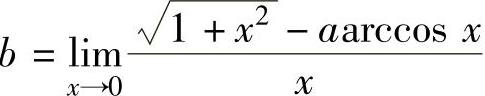 ,从而
,从而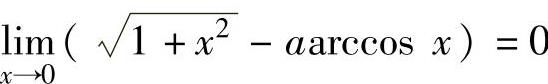 ,由此得
,由此得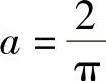 .因此
.因此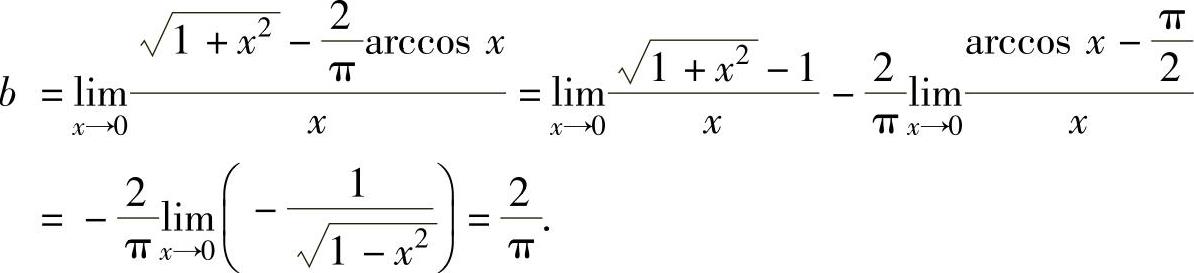
(13)x=-1是f(x)的第二类间断点(无穷间断点);
x=1是f(x)的第一类间断点(可去间断点);
x=0是f(x)的第一类间断点(跳跃间断点).(https://www.xing528.com)
(14)记y1=xsinx,则由lny1=sinx·lnx得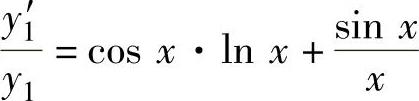 ,所以
,所以
记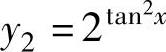 ,则由lny2=tan2x·ln2得
,则由lny2=tan2x·ln2得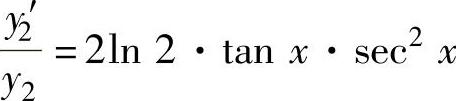 ,所以,
,所以,
因此,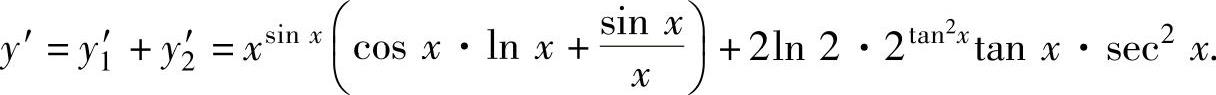
(15)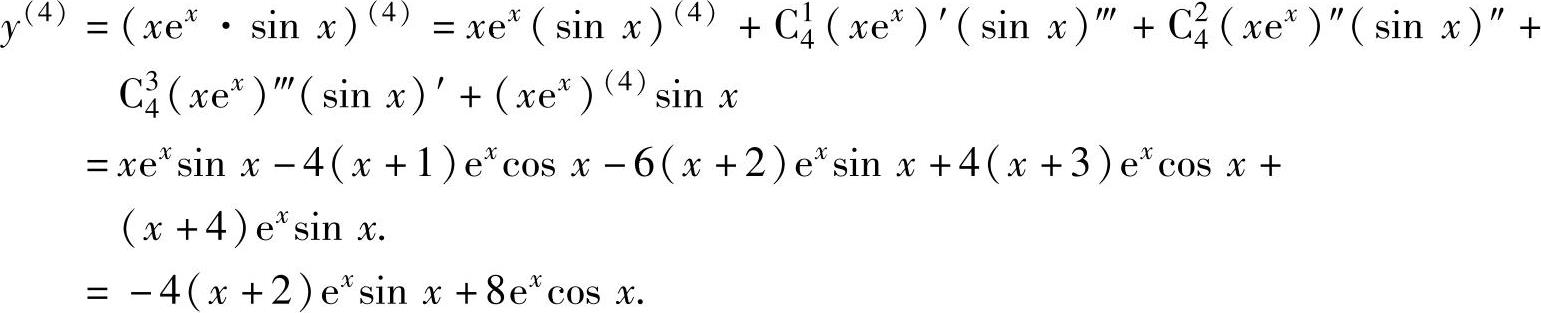
(16)由于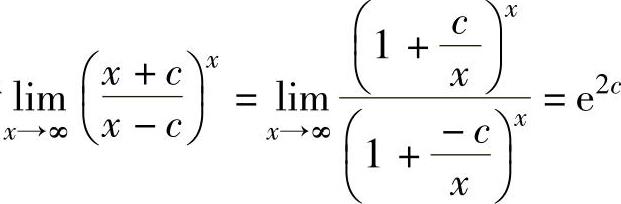 ,
,
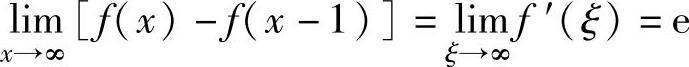 ,所以e2c=e,即
,所以e2c=e,即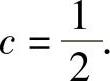
(17)f(n)(x)=(x+n)ex,f(n+1)(x)=(x+n+1)ex,f(n+2)(x)=(x+n+2)ex,由f(n+1)(x)=0得x=-n-1.所以,f(n+2)(-n-1)=e-n-1>0,所以f(n)(x)的极小值为f(n)(-n-1)=-e-n-1.
(18)x<0时,f′(x)=6(x+x2);x>0时,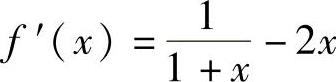 ,此外f(x)在x=0处不可导.于是
,此外f(x)在x=0处不可导.于是
方程f″(x)=0仅有根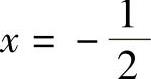 ,且当
,且当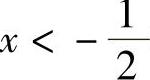 时,f″(x)<0;当
时,f″(x)<0;当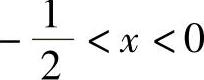 时,f″(x)>0.所以f′(x)有极小值
时,f″(x)>0.所以f′(x)有极小值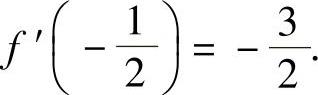
(19)记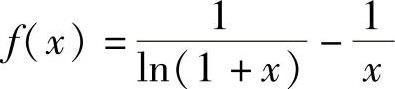 ,则它在(0,1)内可导且
,则它在(0,1)内可导且
记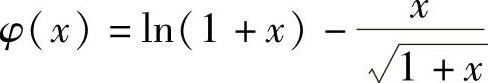 ,它在(0,1)内可导且
,它在(0,1)内可导且
所以,对x∈(0,1),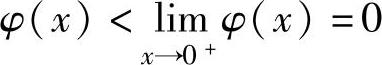 ,从而f′(x)<0.因此
,从而f′(x)<0.因此 ,即
,即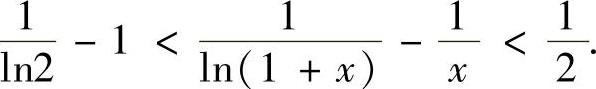
(20)记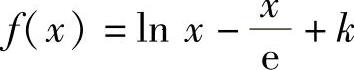 ,则它在(0,+∞)上可导且
,则它在(0,+∞)上可导且
即f(x)在(0,+∞)上的最大值为k.于是,当k<0时,方程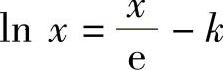 无实根;当k=0时,方程
无实根;当k=0时,方程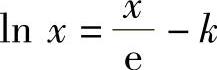 仅有一个实根;当k>0时,注意到
仅有一个实根;当k>0时,注意到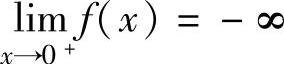 ,
,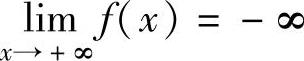 知方程
知方程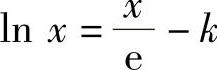 有两个实根.
有两个实根.
(21)作辅助函数F(x)=x2f(x),则F(x)在[0,1]上连续,在(0,1)内可导,且F(0)=F(1)(=0),所以,存在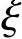 ∈(0,1),使得F′(
∈(0,1),使得F′(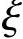 )=0,即
)=0,即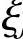 f′(
f′(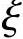 )+2f(
)+2f(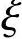 )=0.
)=0.
(22)由于bn-an=nηn-1(b-a)(η∈(a,b)).
所以,nηn-1=n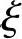 n-1f(
n-1f(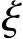 )+
)+ nf′(
nf′(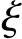 ),即
),即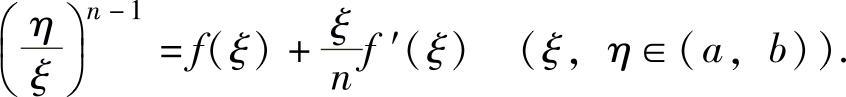
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




