差错控制编码in《计算机网络—原理、技术与应用》

奇偶校验码、循环冗余码是最常用的差错控制编码方法。奇偶校验码是一种通过增加冗余位使得码字中“l”的个数为奇数或偶数的编码方法，它是一种检错码。

衡量编码性能好坏的一个重要参数是编码效率R，它是码字中信息位所占的比例。若码字中信息位为k位，编码时外加冗余位为r位，则编码后得到的码字长度为n=k+r位，由此编码效率R表示为：R=k/n显然，R越大编码效率越高，传送信息码元的有效利用率越高。

1.垂直奇偶校验的特点及编码规则

在面向字符的数据传输中，在每个字符的7位信息码后附加一个校验位“0”或“1”，使整个字符中“1”的个数构成奇数（称奇校验）或偶数（称偶校验）。接收端收到数据后，检查每个字符中“1”的个数是否为奇数（奇校验）或偶数（偶校验），符合则认为传输是正确的。

（1）编码规则

垂直奇偶校验的编码规则（图2-37）

偶校验：r_i=I_1i⊕I_2i⊕…⊕I_pi（i=1，2，…，q）

奇校验：r_i=I_1i⊕I_2i⊕…⊕I_pi⊕1（i=1，2，…，q）

式中，p为码字的定长位数；q为码字的个数

垂直奇偶校验的编码效率为R=p/（p+l）。

（2）校验特点

垂直奇偶校验又称纵向奇偶校验，能检测出每列中所有的奇数个错，但检测不出偶数个的错，因而对差错的漏检率为接近1/2。

【例2-4】发送方要发送字符“hello”，按照ASCII编码，其对应的二进制比特串为

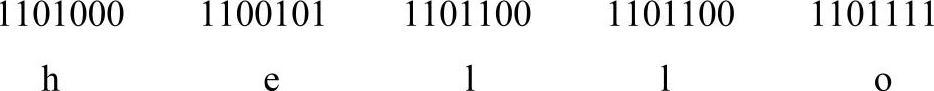
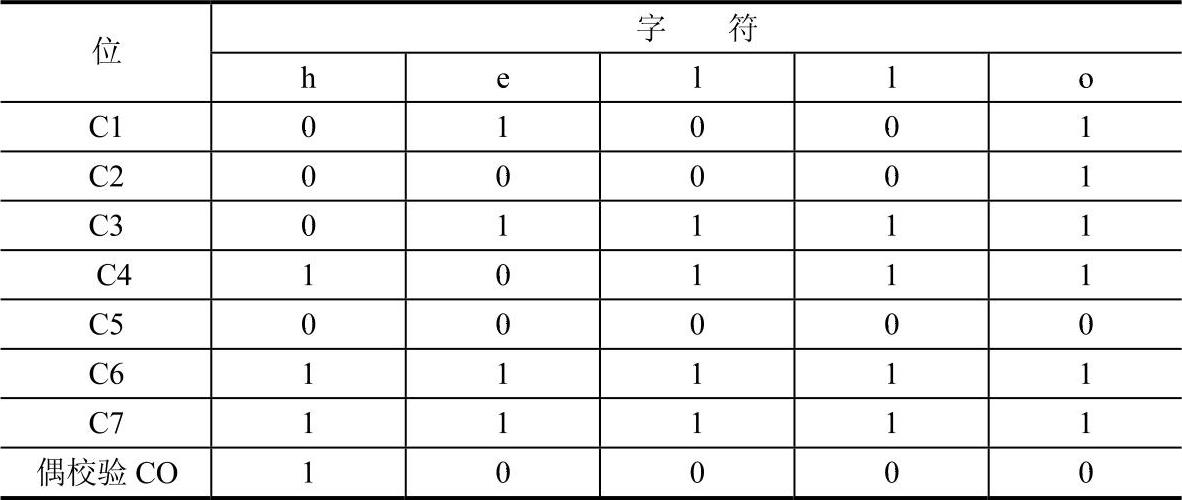
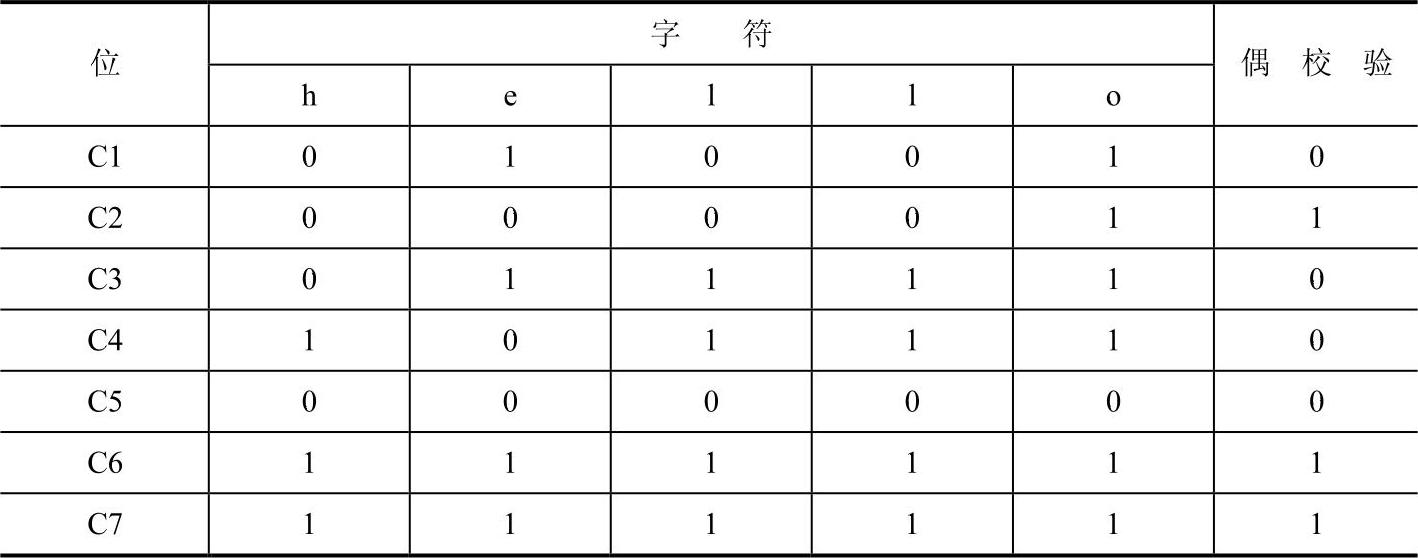
先把数据以适当长度划分组，此处以一个字符ASCII码为一组；然后按字母顺序按列排列，形成一张表；最后在表列方向上附加一个奇偶校验位。此处以偶校验为例，见表2-2。传送时发送的二进制序列为：1101000111001010110110001101100011011110

表2-2 垂直奇偶校验

2.水平奇偶校验的特点及编码规则

在发送字符块末尾附加一个校验字符，该校验字符的第i位是对字符中所有字符的第i位进行奇（或偶）校验的结果。

（1）编码规则

水平奇偶校验编码规则（图2-38）

偶校验：r_i=I_il⊕I_i2⊕…⊕I_iq（i=1，2，…，p）

奇校验：r_i=I_il⊕I_i2⊕…⊕I_iq⊕1（i=1，2，…，p）

式中，p为码字的定长位数；q为码字的个数。

水平奇偶校验的编码效率为R=q/（q+l）。

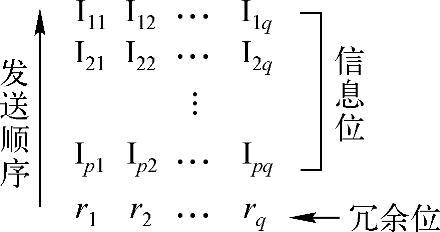
图2-37 垂直奇偶校验的编码规则

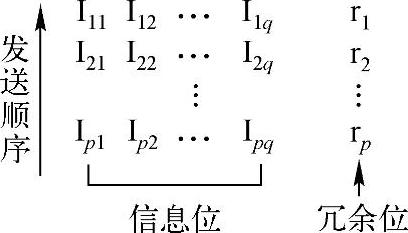
图2-38 水平奇偶校验的编码规则

（2）校验特点

水平奇偶校验又称横向奇偶校验，它不但能检测出各段同一位上的奇数个数的错，而且还能检测出突发长度≤p的所有突发错误。其漏检率要比垂直奇偶校验方法低，但实现水平奇偶校验时，一定要使用数据缓冲器。如发送字符串“hello”，水平奇偶校验见表2-3。仍以偶校验为例。

表2-3 水平奇偶校验

3.垂直水平奇偶校验的特点及编码规则

垂直水平奇偶校验是垂直奇偶校验和水平奇偶校验的综合，即对字符块中每个字符做垂直奇（或偶）校验，再对整个字符块做水平奇（或偶）校验。(www.xing528.com)

图2-39 垂直水平奇偶校验的编码规则

（l）编码规则

垂直水平奇偶校验的编码规则如图2-39所示。

若垂直水平都用偶校验，则

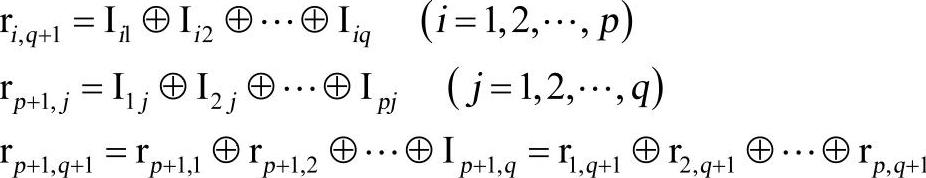
垂直水平奇偶校验的编码效率为R=pq/[（p+l）（q+1）]。

（2）校验特点

垂直水平奇偶校验又称纵横奇偶校验。能检测出所有3位或3位以下的错误、奇数个错、大部分偶数个错及突发长度≤p+l的突发错，可使误码率降至原误码率的百分之一到万分之一，还可用来纠正部分差错。有部分的偶数错不能测出。

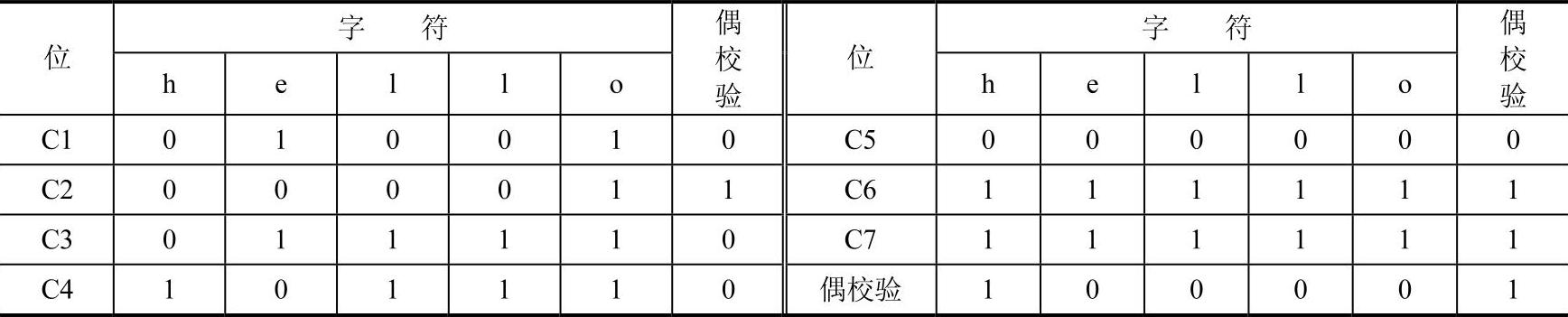
【例2-5】使用垂直水平奇偶校验发送字符“hello”，其编码见表2-4。发送序列为：110100011100101011011000110110001101111011000101

表2-4 垂直水平奇偶校验

4.循环冗余码

（1）循环冗余码的工作原理

网络数据通信中广泛采用循环冗余码（CycleRedundancyCode，CRC），以二进制信息的多项式表示为基础。一个二进制信息可用系数为0或1的一个多项式来表示，如用一多项式K（x）表示一m位信息，可表示为：

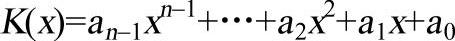
式中，a_i（i=0，1，…，n-l）为二进制数“1”或“0”。比如二进制数110011，可用系数为1、1、0、0、1、1的多项式表示为K（x）=x⁵+x⁴+x+1。

循环冗余码（CRC）在发送端编码和接收端校验时，都可利用事先约定的生成多项式C（x）来得到，k位要发送的信息位可对应于一个（k-l）次多项式K（x），r位冗余位则对应于一个（r-1）次多项式R（x），由r位冗余位组成的n=k+r位码字则对应于一个（n-1）次多项式T（x）=x^rK（x）+R（x）。应用循环冗余码（CRC）能够实现：检测出所有奇数位错；检测出所有双比特的错；检测出所有小于或等于校验位长度的突发错误。

具体的方法是：给信息报文加上一些检查位，构成一特定的待传报文，使之所对应的多项式能被事先指定的多项式除尽。指定的多项式称生成多项式G（x），G（x）由发送方和接收方共同约定。接收方收到报文后，用G（x）检查收到的报文，如用G（x）去除收到的报文多项式，可除尽表示传输无误，否则表明收到的报文不正确，出现错误。

设K（x）表示信息报文的多项式，G（x）为指定的生成多项式，t（x）表示附加了检查位以后的实际传输报文的多项式，那么T（x）应被G（x）除尽。

（2）获得t（x）的步骤

●构成多项式x^rK（x），即在信息报文低位端附加r个0，使它包含（n+r）位，其中n是K（x）的位数，r是G（x）的最高次数。

●求余数R（x）=x^rK（x）/G（x）。求余数的过程是进行异或运算。

●构成一个能被C（x）除尽的T（x）。显然T（x）=x^rK（x）+R（x）一定能被G（x）除尽。

（3）循环冗余码的产生与码字正确性检验实例

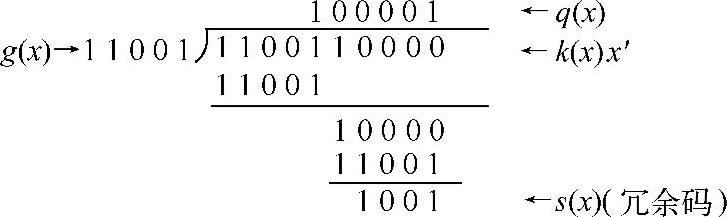
【例2-6】已知信息码为110011，信息多项式K（x）=x⁵+x⁴+x+l，生成码为11001，生成多项式G（x）=x⁴+x³+1（r=4）。求循环冗余码和码字。

解：（x⁵+x⁴+x+1）x⁴=x⁹+x⁸+x⁵+x⁴，对应的码是1100110000。

（x⁹+x⁸+x⁵+x⁴）/G（x）（按异或）。计算结果知冗余码1001，码字是1100111001。

【例2-7】已知，接收码字为1100111001，多项式T（x）=x⁹+x⁸+x⁵+x⁴+x³+1，生成码为11001，生成多项式G（x）=x⁴+x³+1（r=4）。求码字的正确性。若正确则指出冗余码和信息码。

解：用码字除以生成码，余数为0，所以码字正确。

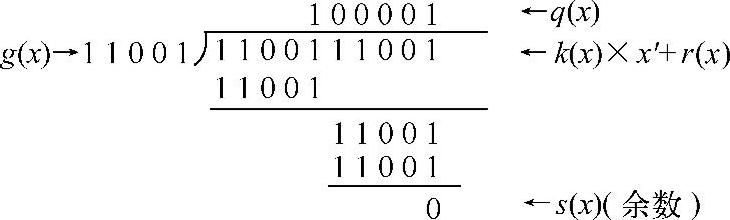
因r=4。所以冗余码是11001，信息码是110011。