对各国纸笔测试的阅读、数学和问题解决成绩与计算机问题解决成绩进行回归分析表明[18],国际平均而言,三个学科成绩可以解释问题解决成绩变异的67.5%,与OECD国际平均的68.0%相当(见下页表4-9)。反过来说,国际平均而言,学生问题解决成绩差异中仍有32.5%的方差是不能通过主要学科领域的成绩来解释的。这显然表明,PISA 2012所测评的学生问题解决能力具有相对的独立性,并非完全受到主要学科领域的影响。
表4-9 纸笔测试的数学、阅读和科学所解释的学生一般问题解决成绩差异
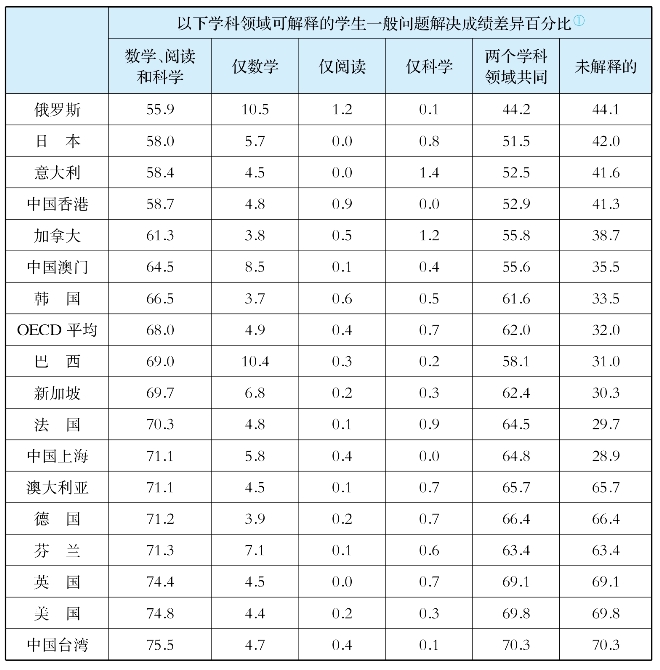
① 此处的方差解释率是通过不同的回归模型计算所得。第二栏、第三栏和第四栏的方差为基于数学、阅读和科学共同解释的方差减去另两个领域共同解释方差之后剩余的部分;未解释的方差是数学、阅读和科学三个学科未能解释的方差;两个学科领域共同解释的方差是数学、阅读和科学所解释的总方差减去三个学科单独解释的方差。
尽管具有相对独立性,但问题解决能力与主要学科之间的关系紧密程度也不相同。具体来说,从OECD平均水平来看,三个学科中数学成绩与学生问题解决能力的关系最为密切,回归系数为0.55;其次是阅读和科学,回归系数分别为0.12和0.18。此外,从相关的紧密程度来说,数学成绩可以单独解释的问题解决成绩变异占4.9%,阅读和科学仅为0.4%和0.7%。这表明学生的数学学习与问题解决能力存在比其他两个主要学科更为密切的关系。
对上海来说,三个主要学科领域和一般问题解决领域呈现出与国际平均相似的特征。具体来说,三个主要领域成绩可以共同解释71.1%的一般问题解决成绩差异。其中,学生数学成绩可以单独解释5.8%,阅读可以解释0.4%,但科学领域的解释率接近0,由两个学科共同解释的占64.8%。(https://www.xing528.com)
上海数学成绩对一般问题解决成绩的回归系数达0.65,显著高于OECD均值0.52;阅读成绩的回归系数为0.17,与OECD平均值没有显著差异。在科学方面,上海学生的回归系数仅为0.05,且不显著,远低于OECD平均值的回归系数0.21(见表4-10)。
表4-10 纸笔测试的数学、阅读和科学与一般问题解决能力的相关

与上海类似,中国香港学生的科学成绩与一般问题解决成绩之间的回归系数也不显著,所有国家或地区中,仅有5个[19]的科学成绩与一般问题解决成绩之间的回归系数不显著。
有趣的是,尽管有8个国家阅读成绩与一般问题解决成绩之间的回归系数都不显著,但仅在新加坡,回归系数是负数。相应的新加坡学生数学成绩与问题解决成绩之间的回归系数达到0.77,远高于排在其后的巴西的0.68。这表明,新加坡学生的数学成绩与问题解决成绩之间的关系更为密切。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




