基于PISA的学生问题解决能力研究

直到目前，纸笔测试仍是最为常见的测试方式。在PISA 2015年之前，几乎所有主要领域的测试都是基于纸笔进行的，基于计算机的测试主要作为选项进行。从2015年开始，尽管主要学科领域开始采用计算机进行测试，但其中绝大部分的测试内容仍采取的是基于纸笔的二维呈现。这些题目不仅包括原有的链接试题，还包括新开发的静态（Static）试题。数学作为PISA 2012的主要评估领域，是以纸笔测试的方式呈现的，尽管在PISA 2015中数学将以计算机的方式进行评估，但主要是将原有的链接试题移植到计算机上。

3.2.1.1　基于数学问题解决描述的评估框架

根据PISA数学素养的界定，数学领域的测评虽然包含对数学基本概念、事实和技能的掌握，但一般都不会直接考查这些内容，而是将这些数学内容嵌入具体的问题情境中，通过学生解决问题的过程来评估他们在真实情景中运用这些知识和技能的能力。

PISA 2012的素养结构图显示的更为清晰（见图3-4）。学生的数学素养清晰地描述为一个环形，环形的开端是一个处于情境中的问题，学生首先要将其以数学的形式表述出来，即转化为一个数学的问题；然后通过运用数学的事实和工具解决这一问题并获得一个数学结果；数学结果必需结合情境再次转化为一个情境中的结果；进而对该结果进行评估，判断其是否适合最初的问题情境。

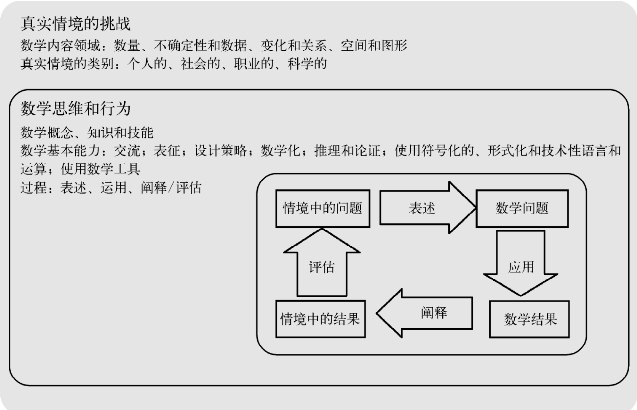
图3-4　PISA 2012数学素养测评框架示意图^[25]

3.2.1.2　真实和有意义的数学问题情境

PISA数学素养的一个重要特征是数学内容被置于真实的问题情境中。数学问题情境（Context）是指解决问题涉及的所有要素共同构成时空背景。PISA将问题情境视为问题所处的个人世界的不同侧面。为此，PISA分析了个体针对不同学科内容可能遇到的广泛的问题背景，并对其进行划分。按照与个体由近及远的顺序，数学问题情境包括“个人的、社会的、职业的、科学的”四个主要类别。个体的是指个人或家庭日程生活情境，例如已公开样题中的“海伦骑自行车”“调味汁”等；社会的是指个体所生活的社群，可以是社区，也可以是更大范围的国家或世界，例如已公开样题中的“唱片排行榜”“度假别墅”“有线电视”等；职业的是指与工作相关的情境，例如“木匠”“卖报纸”等；科学的是指在科学或技术中运用数学的情境，例如“风筝帆船”“风力发电”等。按照PISA 2012的评估框架，四类情境所对应的试题数量应各占1/4。

除了对真实性和广泛性的强调，PISA还要求问题情境对学生而言是“有意义”的。也就是说，对于15岁的学生而言，问题情境应该是适当的，与其生活相关的，能引起学生的兴趣的。这与数学教学必需与学生实际紧密结合的一般教学规律是相一致的。15岁的学生限于生活和经验，还不可能对现实生活的众多领域有非常深入的理解，因此，问题情境不宜过于生僻，应该是绝大多数学生在课堂或课外生活中能够接触或可以理解的。例如，房屋装修的问题对绝大多数15岁学生来说是一个陌生领域，如果简单要求学生依据经验计划或核算房屋装修费用，显然并不适当，但如果将其简化为计算瓷砖铺设面积、油漆用量等学生可以理解的问题，就能较好激发学生解决问题的兴趣。

PISA测评的目的是考查学生是否为未来生活做好准备，希望评估他们在面对现实世界的挑战时有效地运用所学的知识和技能的能力。因此，数学问题不仅限于学校和书本，绝大部分来自广泛的现实领域，这与我国中小学通常使用的数学题目非常不同，也与国际上其他类型的测试，例如TIMSS数学测试有很大区别。通过对广泛数学问题情境的分析，PISA数学试题很好地覆盖了15岁学生可能应用数学的各种主要情境，反映了学生数学应用的全貌。

3.2.1.3　全面覆盖的数学知识领域

要解决数学问题，学生必需首先具备一定的数学知识。通常情况下，学校的数学课程是按照数学知识来组织的，知识的教授顺序也是按照学科知识的内部逻辑来安排。但真实的数学问题往往都是各种因素相互交织在一起。学生要解决一个问题，必需首先判断应该利用哪些已经掌握的数学知识，并对问题进行适当的数学式表述。所以，有必要对15岁学生所应掌握的数学内容划分，以使数学题目较好的覆盖整个数学学科领域。PISA 2012的数学内容领域包括“变化和关系”“空间和图形”“数量”以及“不确定性和数据”四个方面。

●变化和关系（Change and Relationship）是利用适当的函数或方程进行建模，创造符号或图示来表征关系，阐释这些表征并在表征间相互转换。该领域与传统的代数和函数内容相似。

●空间和图形（Space and Shape）不限于传统几何学的范畴。包括诸如理解透视（例如绘画时）、制图与读图、图形转换、阐释不同视角下的三维场景以及形成图形的表征。该领域接近传统的几何领域。

●数量（Quantity）是描述和测量现实世界多种特征类别的主要方法。要采取量化的手段，需要理解测量、计数、量级、单位、指标、相对大小、数的趋势和模式。数量推理是该领域数学素养的核心，包括诸如数感、数的不同表征、计算、心算、估算和评估结果合理性。

●不确定性和数据（Uncertainty and Data）主要对应传统课程领域的概率和统计内容。科学、技术和日常生活中都存在着不确定性，因此，不确定性和数据是利用数学对许多问题情境进行分析的核心。认识到计算中变异的重要性、对变异量的感知，认识到测量的误差和不确定性，懂得机会的含义，都属于本领域的内容。

3.2.1.4　完整的数学问题解决过程

PISA 2012依据个体数学问题的解决步骤来划分数学过程，这与PISA 2003将数学过程区分为“再现”“联系”和“反思”三个由简单到复杂的“能力群”的方法显然不同。PISA 2012认为数学素养是个体的数学表述、数学应用和数学阐释能力。它们提供了一个组织数学问题解决过程的良好且有意义的结构，分别描述了个体将问题与数学相连接的过程、解决数学问题的过程和将对数学结果进行交流、评判的过程。

●数学表述（Formulating）是指将真实世界的情境转换为数学情境，并为真实问题提供数学结构、表征和清晰陈述，进行推理并弄清问题中的限制条件和假设。(www.xing528.com)

●数学运用（Employing）是指个体能够运用数学概念、事实、步骤和推理以解决数学问题，并获得数学结论的过程。

●数学阐释（Interpreting）关注的是个体对数学解答、结果和结论的反思以及在真实的问题情境中进行阐释。它包括转换数学答案或返回到问题情境，进而判定结果是否合理、在问题情境中是否有意义。

数学问题解决过程划分为三个阶段并非表明数学问题的解决过程仅包括三个阶段，而是为了测试便于操作化。实际上，每个解决过程还可以再细化为不同的部分。例如，数学阐释不仅包括对已获得的数学结果进行反思，还包括将数学结果返回到问题情境，进而判断其合理程度。并且，数学阐释不仅发生在数学问题解决后，在问题解决的中间过程也需要不断地通过反思来调整使用的策略和数学概念、定理和论证，以确保问题解决向正确的方向推进。

3.2.1.5　嵌入问题解决过程的数学基本能力

PISA强调学生解决真实数学问题的能力，并非忽视学生对抽象数学概念的理解以及对纯数学内容，如数学推理、数学原理和法则、数学论证等的掌握。实际上，PISA非常强调这些数学的基本能力。这是因为，随着计算机的普及，数学应用中的常规运算已经可以被机器替代，与此相应的，生活中大量的问题都要求人们对数学有一定程度的理解，进而通过数学推理做出判断。换句话说，对个人生活而言，数学的重要意义越来越多地体现为提供理性判断和推理逻辑，而非运算能力。PISA 2012数学素养特别指出采用“数学式的推理，以及使用数学概念、步骤、事实和工具来描述、解释和预测现象”^[26]，而在此之前，PISA数学素养概念没有明确指出这一点，这体现出PISA对抽象数学内容的重视。

PISA 2012在PISA 2003的基础上对数学基本能力进行了修订，认为共包含7种基本能力，分别是：交流，数学化、表征能力，推理和论证，设计问题解决策略，使用符号化、形式化和技术性的语言和运算，使用数学工具。与PISA 2003相比，新框架建构的数学基本能力采用含义更广的数学化的概念代替了建模，采用推理和论证综合了思考和推理能力，采用设计策略代替了问题提出与解决，采用使用数学工具代替了使用辅助设备和工具。

交流　既包括接收过程也包括表达过程。个体通过对陈述、问题、任务或目标的阅读、解码和阐释，形成对问题条件的心理模型。问题解决之后，个体可能需要呈现或解释问题解决方法。

数学化　是在现实世界和数学世界之间的移动。它包含表述和阐释两个部分。讲一个问题表述为一个数学问题会包括结构化、概念化、提出假设和/或建构模型。阐释包括判断数学的结果是否或在多大程度上与原有的问题情境相关联，还包括判断结果的准确性。数学化直接与框架中的表述和阐释相联系。

表征能力　需要在不同表征间进行选择、阐释和转换，还需要用不同表征来说明一个情境、与问题相互作用或呈现完成的工作。所指的表征包括数据图、数据表、示意图、图片、等式、公式、文字描述和真实材料。

推理和论证　遍布在数学素养相关的不同过程和不同活动。该能力包括逻辑基础的思维过程，借助它可以探索并将问题要素相互连接以便做出推论，检查给定理由和合理性，或为问题的表述和解决方法提供理由。

设计问题解决策略　是指选择或设计一个计划和策略，用数学来解决任务和情境中的问题，并且引导和监督其实施过程。它包括在多种多样的数据中寻找联系以便整合信息并高效解决问题。

使用符号化、形式化和技术化的语言和运算　包括理解、阐释、操作和利用符号和算数表达式及运算，使用有明确定义、规则和公式体系的公式，以及在上述内容中使用运算法则。

使用数学工具　包括了解并能够使用不同的工具（有形工具和数字化工具）来协助进行数学活动，并且了解这些工具的限制条件。PISA基于计算机的数学测试选项扩大了学生使用数学工具的可能性。

大多数传统的数学测试中也非常重视数学基本能力，特别是抽象的数学概念、数学推理、数学表征，然而，大多数评估都以抽象的方式来评估这些能力。PISA同样重视抽象的数学内容，但并非简单通过抽象的数学试题或数学公式推演来呈现，而是将基本能力嵌入在生活问题的解决过程中。也就是说，在PISA中抽象的数学内容和推理大都隐含在具体的问题中。我们以样题“伦敦眼”为例来说明（见图3-5）。

问题情境为摩天轮的图片、示意图以及文字描述“摩天轮的外部直径为140米……”问题要求学生计算摩天轮的中心点M比河面高出多少米。不难看出，该问题考查学生是否理解圆的直径和半径的概念，但抽象的数学概念完全转化为了具体的数学问题。学生要解决这一问题，需要真正理解直径和半径的概念，知道M点高出河面的距离就是圆的半径加摩天轮高出水面的距离，相比“圆的直径为140米，半径多少米”这样抽象的提问，该题更能评估学生对数学概念的真正掌握。

图3-5　PISA样题“伦敦眼”