ANSYS14.0有限元分析：特点全揭秘

（1）对于复杂几何构形的适应性：由于单元在空间上可以适用一维、二维或三维的，而且每一种单元可以有不同的形状，同时各种单元可以采用不同的连接方式，所以，工程实际中遇到的非常复杂的结构或构造都可以离散为由单元组合体表示的有限元模型。图1-4所示为一个三维实体的单元划分图。

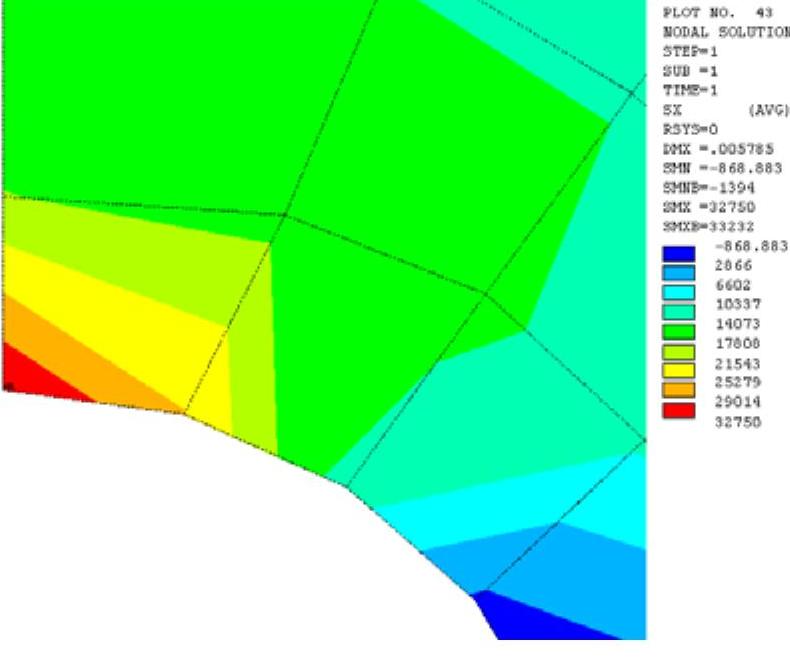
（2）对于各种物理问题的适用性：由于用单元内近似函数分片地表示全求解域的未知场函数，并未限制场函数所满足的方程形式，也未限制各个单元所对应的方程必须有相同的形式，因此它适用于各种物理问题，例如线弹性问题、弹塑性问题、粘弹性问题、动力问题、屈曲问题、流体力学问题、热传导问题、声学问题、电磁场问题等，而且还可以用于各种物理现象相互耦合的问题。图1-5所示为一个热应力问题。

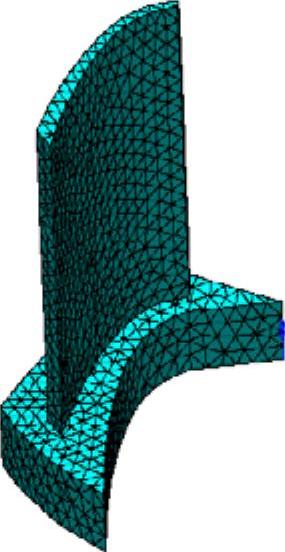
图1-4 三维实体的单元划分模型

(www.xing528.com)

图1-5 热应力问题

（3）建立于严格理论基础上的可靠性：因为用于建立有限元方程的变分原理或加权余量法在数学上已证明适微分方程和边界条件的等效积分形式，所以只要原问题的数学模型是正确的，同时用来求解有限元方程的数值算法是稳定可靠的，则随着单元数目的增加（即单元尺寸的缩小）或者是随着单元自由度数的增加（即插值函数阶次的提高），有限元解的近似程度不断地被改进。如果单元是满足收敛准则的，则近似解最后收敛于原数学模型的精确解。

（4）适合计算机实现的高效性：由于有限元分析的各个步骤可以表达成规范化的矩阵形式，最后导致求解方程可以统一为标准的矩阵代数问题，特别适合计算机的编程和执行。随着计算机硬件技术的高速发展以及新的数值算法的不断出现，大型复杂问题的有限元分析已成为工程技术领域的常规工作。