随着瓦特改进蒸汽机使热机的效率大为提高,人们对进一步提高热机效率的要求也日益迫切.法国青年工程师卡诺提出了一个理想循环,在他提出的循环过程中,工作物质只和两个恒温热源交换热量,这种循环被称为卡诺循环,按卡诺循环工作的热机叫卡诺热机.
卡诺循环是由四个准静态过程所组成的,其中有两个是等温过程,两个是绝热过程.卡诺循环对工作物质是没有规定的,为方便讨论,我们以理想气体为工作物质,如图8.5 所示.曲线12 和34分别是温度为T1 和T2 的两条等温线,曲线23 和41 分别是两条绝热线.作为工作物质的理想气体从状态1 出发,按顺时针方向沿封闭曲线12341 进行,这种正循环为卡诺正循环,又称卡诺热机.由于每个过程都做功,如果利用功进行计算比较麻烦,考虑到绝热过程不吸热的特点,这里利用热量来求热机效率.

图8.5 卡诺循环示意图
1→2 等温膨胀:气缸中的气体与温度为T1 的高温热源接触,等温地由体积V1 膨胀到V2,该过程中吸热为

2→3 绝热膨胀:气体绝热膨胀,体积由V2 增大为V3,温度由T1 降为T2.
3→4 等温压缩:气体与温度为T2 的低温热源接触,体积由V3压缩到V4,该过程中气体放热为

4→1 绝热压缩:气体绝热压缩,体积由V4 变为V1、温度由T2升至T1,完成整个循环.
根据热机效率的定义,卡诺热机的效率为

又由于2→3、4→1 均为绝热过程,根据绝热过程方程
![]()
整理可得

于是有

此即理想气体准静态卡诺循环的效率.要完成一次卡诺循环必须有高温和低温两个热源;卡诺热机的效率与工作物质无关,只与两个热源的温度有关,高温热源的温度越高,低温热源的温度越低,则卡诺循环的效率越高.

如果理想气体沿相反的方向进行循环过程,在一个循环中,系统从低温热源T2 处吸热Q2,向高温热源T1 放热Q1,外界对系统做功A=Q1-Q2,则这是一个制冷循环.该循环的制冷系数为以理想气体为工作物质的卡诺制冷机,高温热源温度T1 越高,低温热源温度T2 越低,制冷系数越小,表明从温度较低的热源吸取热量越困难,而当两热源温度越接近,低温热源温度越高,制冷系数越大.
例8.4 1 mol 氦气经过如图8.6 所示的循环,其中p2=2p1,V4=2V1,求在每个中间过程中气体吸收的热量,如果循环按照1→2→3→4→1 进行,求循环的效率.
解 由图8.6 可知:p2 =p3 =2p1 =2p4,V3 =V4 =2V1=2V2,根据理想气体物态方程可以分别求得状态2、3、4 的温度为
![]()
可见,在等体过程1→2 及等压过程2→3 中氦气分别吸热Q12和Q23;在等体过程3→4 及等压过程4→1 中分别放热Q34和Q41,对于单原子分子氦气,其CV,m=![]() 由式(8.10)和式(8.13),可得
由式(8.10)和式(8.13),可得
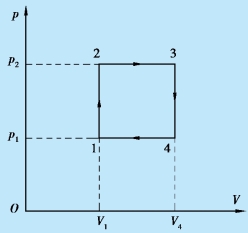
图8.6 例8.4 用图

所以氦气经历一个循环吸收的热量之和为
![]()
氦气在此循环中放出的热量之和则为
![]()
如果循环按照1→2→3→4→1 进行,此循环的效率为
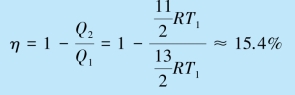
例8.5 一定量的某单原子分子理想气体,经历如图8.7 所示的循环,其中AB 为等温线.已知V1=3.0×10-3 m3,V2=6.0×10-3 m3,求热机效率.(https://www.xing528.com)
解 如图8.7 所示的循环由3 个分过程组成:
(1)A→B 为等温膨胀过程,ΔE=0,A>0,吸收热量

图8.7 例8.5 用图
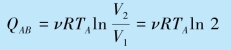
(2)B→C 为等压压缩降温过程,ΔE<0,A<0,放出热量
![]()
(3)C→A 为等体增压升温过程,ΔE>0,A=0,吸收热量
![]()
由B→C 的过程方程知

且由题意知
![]()
所以有
![]()
又因单原子分子理想气体的定体摩尔热容![]() 故
故
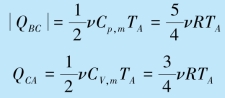
于是在所讨论的循环中,系统从高温热源吸热
![]()
向低温热源放热

故热机效率为
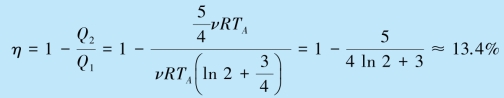
例8.6 一台电冰箱放在室温为20 ℃的房间里,冰箱储藏柜中的温度维持在5 ℃.现每天有2.0×107 J 的热量自房间传入冰箱内,若要维持冰箱内温度不变,外界每天需做多少功?其功率为多少?设在5 ℃至20 ℃运转的冰箱的制冷系数是卡诺制冷机制冷系数的55% .
解 工作在高温热源T1=293 K 和低温热源T2=278 K 之间的卡诺制冷机的制冷系数
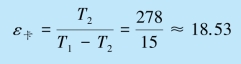
该冰箱实际的制冷系数为
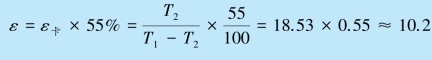
由制冷机制冷系数的定义![]() 得
得

房间传入冰箱的热量Q′=2.0×107 J,平衡时Q′=Q2,保持冰箱在5 ℃至20 ℃运转,每天需做功
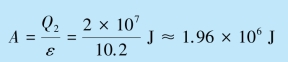
所以其功率为
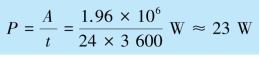
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




