大学物理学（上册）：功、热量和内能

通过做功可以改变系统的状态.在做功的过程中，外界与系统之间进行能量的交换，从而改变系统的机械能.热力学的平衡态要满足力学、热学和化学平衡条件，将力学平衡条件被破坏时产生的对系统状态的影响称为力学相互作用.在力学相互作用的过程中，系统与外界转移的能量就是热力学的功.这种力是一种广义的力，不仅包含机械力，也包含电场力、磁场力等；相应的，功也是广义的功，除包括机械功外，还可以有电场功、磁场功等.

在功的计算方面，力学中只要知道力作为位置坐标的函数和质点运动的路径即可通过积分求出力所做的功.对准静态过程，把广义的力表达为状态参量的函数，利用广义力对应的广义的位移，就能计算出相应的功.

下面讨论汽缸内的气体由初始状态（p1，V1）准静态地变化到末了状态（p2，V2）的过程中，系统对外界所做的功.

如图8.1 所示，立方形的汽缸内有一无摩擦且能左右滑动的截面积为S 的活塞，里边封闭一定质量的气体.活塞施于气体的压强为pe，则在活塞移动距离dx 的无限小过程中，活塞对气体做的元功dA′为

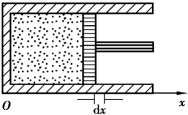
图8.1　气体膨胀做功示意图

式中，dV 表示体积改变量，在准静态过程中，系统和外界要始终处于力学平衡，外界施予气体的压强pe 等于气体的压强p；考虑到力的方向，则在该过程中，气体系统对外界做的功dA 为

当系统从初态（p1，V1）变化到末态（p2，V2），该过程中系统对外界所做的功A 为

根据该式可知：(www.xing528.com)

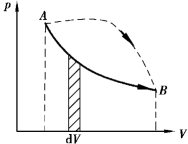
图8.2　功的示意图

（1）准静态过程中系统对外界做的功，可以用系统的状态参量p 对状态参量V 的积分给出.这里广义的力为压强p，广义的位移为体积V.

（2）式（8.1）是无限小的过程中气体对外界所做元功的表达式.若dV>0，则dA>0；若dV<0，则dA<0.表明系统膨胀时对外界做正功，被压缩时，系统对外界做负功.

（3）式（8.2）的结果依赖于过程中压强与体积的关系，即p（V）的表达式，它表明功是一个和具体过程密切相关的过程量，而不是由系统的状态所确定的状态量.在无限小过程中，系统对外界是否做功、做正功还是做负功，完全可根据系统体积的无限小变化确定.但对于有限的热力学过程，不能根据初态体积与末态体积的相对大小来判定系统对外界所做功的正负.因为功与具体过程密切相关，而并非决定于始末状态.

准静态过程中，系统对外界做的功可以在p-V 图上直观地表示出来，如图8.2 所示.在无限小过程中，式（8.1）表示的元功dA的大小等于V～V+dV 过程曲线下的“面积”，式（8.2）表示的整个过程中系统所做功等于A ～B 曲线下的“面积”的代数和.对一定的系统，当过程的初态和末态确定时，连接初态和末态的过程曲线可以有无穷多条，不同的过程曲线下的面积不完全相同，可以直观地表明功是过程量.

如果状态的改变源于热学平衡条件的破坏，即系统与外界存在温度差，这时系统就与外界存在热学相互作用，作用的结果是有能量从高温物体传递到低温物体，这个传递的能量就是热量.系统经不同的热力学过程从同一初态过渡到同一末态时，系统从外界吸收的热量是不同的，与具体的热力学过程有关.热量和功是系统状态变化过程中伴随发生的两种不同的能量传递形式，它们都与中间经历的过程有关，热量和功都是过程量.

热量的本质是历史上长期争论过的问题，历史上存在“热质说”和“热来源于运动”两种截然不同的观点.热质说认为，热是一种能渗入一切物体之中且看不见的不生不灭的无重流体物质.热的物体含有较多的热质，冷的物体含有较少的热质，冷热不同的物体热接触，热质从较热的物体流向较冷的物体，在热传递过程中热质守恒.伦福德用实验事实（用钝钻头加工炮筒时摩擦生热）否认了热质说的错误观点，从而支持了热来源于运动的学说.焦耳实验表明，一定热量的产生（或消失）总是伴随着等量的其他形式的能量消失（或产生），并不存在单独守恒的热质.

大量实验精确地表明，系统从同一初态过渡到同一末态时，在各种不同的绝热过程（与外界没有热量交换的过程）中，外界对系统所做的功是一个恒量，该功与具体实施的绝热过程无关，仅由始、末状态决定.

绝热过程中外界对系统做功的这种特性与重力做功有相似之处，重力的功只与物体的始、末位置有关而与运动的路径无关，由此引入了重力势能；根据绝热功的特点，引入一个与系统的状态相对应的能量——内能，当系统绝热地从初态过渡到末态时，系统内能的增量等于外界对系统所做的绝热功.内能E 是一个由系统的状态确定的函数，是态函数.上述关于内能的定义，实际上定义的是始、末两态内能的差，内能的值可以有一个任意的附加常数.

以上是从宏观力学的观点，即绝热系统与外界之间交换的能量来说明内能；从微观的角度看，内能是系统内部所有微观粒子的微观无序运动能量以及总的相互作用势能之和.内能是态函数，处于确定的平衡态的系统，其内能亦是确定的，即内能与状态之间有一一对应的关系.态函数和过程量具有完全不同的性质，态函数仅由系统的宏观状态决定.在任一平衡态下，态函数都可表达为系统状态参量的函数；当系统状态变化时，态函数亦相应发生变化；当系统的始、末两态确定后，态函数的增量是完全确定的.