1)平均速率
大量分子运动速率的算术平均值称为平均速率,用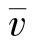 表示,它的定义式为
表示,它的定义式为
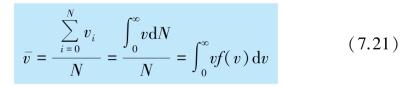
将麦克斯韦速率分布函数式(7.20)代入式(7.21),可得平衡态下理想气体分子的平均速率为

2)方均根速率
大量分子无规则热运动速率二次方的平均值的平方根称为方均根速率,表示为

把麦克斯韦速率分布函数式(7.20)代入式(7.23),计算可得

3)最概然速率
从f(v)与v 的关系曲线图中可以看出,f(v)有一最大值,与f(v)的极大值相对应的速率称为最概然速率,用vp 表示.vp 的物理意义是:在平衡态条件下,理想气体分子速率分布在vp 附近单位速率区间内的分子数占气体总分子数的比例最大.根据极值条件 成立,把麦克斯韦速率分布律式(7.20)代入极值条件可得最概然速率为
成立,把麦克斯韦速率分布律式(7.20)代入极值条件可得最概然速率为

最概然速率vp 是反映速率分布特征的物理量,并不是分子运动的最大速率.同一种气体,当温度增加时,最概然速率vp 向v 增大的方向移动,如图7.7 所示.在温度相同的条件下,不同气体的最概然速率vp 随着分子质量m 的增大而向v 减小的方向移动.
由上述三种速率公式可以发现,三种速率都含有统计平均的意义,对少量分子无意义,它们都与 成正比,与
成正比,与 成反比.在同一温度下三者大小之比为
成反比.在同一温度下三者大小之比为![]() 由此可知,
由此可知,![]() 如图7.8 所示.
如图7.8 所示.
这三种速率,就不同的问题有着各自的应用.在讨论速率分布时,要用大量分子的最概然速率;计算分子运动的平均距离时,要用平均速率;而计算分子的平均平动动能时,则要用方均根速率.

图7.8 同一温度下的三种速率
例7.5 计算在27 ℃时,氢气和氧气分子的方均根速率vrms.
解 已知氢气和氧气的摩尔质量分别为![]() 又知R=8.31 J/(K·mol),T=300 K,把它们分别代入方均根速率公式
又知R=8.31 J/(K·mol),T=300 K,把它们分别代入方均根速率公式![]() 可得氢分子的方均根速率vrms≈1.93×103 m/s,氧分子的方均根速率
可得氢分子的方均根速率vrms≈1.93×103 m/s,氧分子的方均根速率![]()
从以上数值可以看出,通常温度下气体分子的方均根速率是很大的,一般在数百米每秒.在力学中我们已经知道,地球表面附近的物体要脱离地球引力场的束缚,其逃逸速率为11.2 km/s.这个速率为氢分子的方均根速率的6 倍.这样一来似乎在地球的大气层中有可能存在大量的自由氢分子.然而,从观测中发现在地球的大气层中几乎没有自由的氢分子.这是为什么呢?
从麦克斯韦分子速率分布曲线图7.7 可以看出,有相当数量的气体分子的速率比方均根速率要大得多,当这些分子的速率达到逃逸速率时,它们将逃逸出地球的大气层,因为不断有氢分子逸出大气层,所以在地球大气层中自由的氢分子就为数很少了,可以认为大气层不存在自由的氢分子.另一方面,氧分子的方均根速率只约为氢分子的方均根速率的1/4,且只有很少的氧分子能达到逃逸速率,所以在地球大气层中能找到较多的自由氧分子.同样,与氧分子质量差不多的氮分子,也很少能逃逸出地球大气层.
实际上,大气气体成分形成现在的比例的原因是很复杂的,许多因素还不清楚.根据1963 年人造卫星对大气上层稀薄气体成分的分析,证实在几百千米的高空,其上有一层“氢层”,实际上是“质子层”.
例7.6 假定有N 个气体分子,它们的速率分布不遵从麦克斯韦速率分布,而是如图7.9 所示(当v>2v0 时,粒子数为零).(https://www.xing528.com)
(1)用N 和v0 表示出b;
(2)求速率在1.5v0 和2.0v0 之间的分子数;
(3)求速率介于1.5v0 和2.0v0 之间的分子的平均速率;
(4)求全部分子的方均根速率.
解 (1)由速率分布函数归一化条件![]() 1 知
1 知

图7.9 例7.6 用图
由图知

积分解得
![]()
(2)由![]() 得,dN=Nf(v)dv,介于在1.5v0 和2.0v0 之间的分子数可以用下面式子求得
得,dN=Nf(v)dv,介于在1.5v0 和2.0v0 之间的分子数可以用下面式子求得

(3)平均速率公式![]() 介于在1.5v0 和2.0v0 之间分子的平均速率可用下式求得
介于在1.5v0 和2.0v0 之间分子的平均速率可用下式求得

(4)气体分子的方均根速率
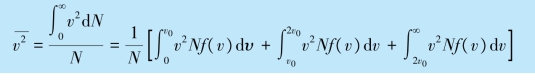

例7.7 求速率大小在vp 与1.01vp 之间的气体分子数占总分子数的比率.
解 因为
令
这里x=1 、Δx=0.01 ,所以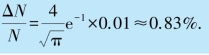
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




