自由度是物体运动的自由程度.固定在空间某点处的质点,完全丧失了运动的自由,其自由度为零;约束在空间某一直线或曲线上的质点,物体只能沿定直线或定曲线运动,其自由度为1,物体的位置用一个位置坐标x 或s 即可确定;限制在一个平面上的质点,可以独立地沿两个相互垂直的方向运动,如沿x 轴和y 轴方向运动,其自由度为2,物体的位置可由质点的位置坐标x 和y 确定.由此可见,物体运动的自由程度与确定物体空间位置的独立的坐标数目有密切关系,是可以定量化的.确定物体在空间的位置所必需的独立坐标的数目称为物体的自由度.
单原子分子可视为在三维空间运动的质点,要确定其空间位置,需要3 个坐标,如x、y、z,其自由度为3,这三个自由度称为平动自由度.
双原子分子,如果原子间的相对位置不变,那么,该分子就可看作由保持一定距离的两个质点组成.这种分子称为刚性双原子分子,即哑铃式双原子分子组成的,如图7.3(a)所示,两原子m1和m2 之间的距离,在运动过程中可视为不变,这就好像两原子之间有一根质量不计的刚性细杆相连.设点C 为双原子分子的质心,并选如图7.3(b)所示的坐标轴.于是,双原子分子的运动可看作质心C 的平动,以及通过点C 绕y 轴和z 轴的转动.
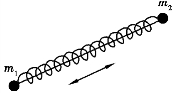
由于质心位置需要3 个独立坐标决定,它们属于平动自由度;通过质心C 绕y 轴和z 轴的转动需用2 个独立坐标决定,这两个是转动自由度,所以刚性双原子分子共有5 个自由度.如果两个原子间的距离是随时间而改变的,就好像在原子间被一根质量可略去不计的弹簧相连,如图7.4 所示.这种双原子分子称为非刚性双原子分子.非刚性双原子分子在刚性双原子分子的基础上再增加一个振动自由度,所以非刚性双原子分子共有6个自由度.
对于3 个及3 个以上原子构成的多原子分子,如果原子间的距离保持不变,分子被称为刚性多原子分子.这里考虑一般情况,即刚性多原子分子为非线性分子.刚性多原子分子可以用刚体模型来处理.刚体的运动一般可分解为刚体随质心的平动和绕质心的转动,如图7.5 所示.确定质心坐标需要3 个独立坐标,因此质心具有3 个平动自由度.接下来考虑刚体的转动自由度.首先确定转轴的方位,转轴的方位需要3 个方位角(α、β、γ)来表示,但3 个角度并不相互独立,由关系式cos2α+cos2β+cos2γ=1 来约束,因此确定转轴方位的独立坐标只有2 个.确定转轴后,刚体还可以绕轴转动,因此还需要一个1 个转动自由度.因此刚体具有3 个平动自由度,3 个转动自由度,共需要6 个自由度.

图7.3 刚性双原子分子
 (https://www.xing528.com)
(https://www.xing528.com)
图7.4 非刚性双原子分子
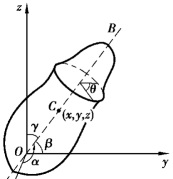
图7.5 刚体的运动
如果原子间距离随时间变化,这些分子被称为非刚性多原子分子.如果有N 个原子构成的非刚性多原子分子(非线性),它的自由度最多有3N 个,其中平动自由度为3 个,最多有3 个转动自由度和3N-6 个振动自由度.如果在本书中不作特别说明,双原子分子或多原子分子都作为刚性分子处理.
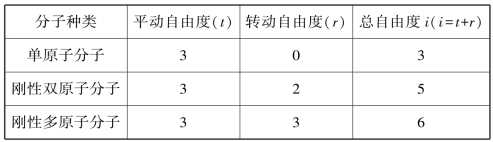
气体分子的自由度数如表7.1 所示.
表7.1 气体分子的自由度数
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




