大学物理学上册：理想气体的压强

气体作用在器壁上的压强是大量分子对容器壁不断碰撞产生的综合效果.虽然单个分子碰撞器壁的作用是短暂的、微弱的、间歇性的，但大量分子碰撞的结果就表现为宏观、均匀而持续的压力.生活中都有这样的经验，当撑着雨伞在大雨中行走时，我们会感觉到由于密集的雨点打在雨伞上所产生的压力.其实，构成气体的大量分子与容器壁碰撞产生的效果与雨点打在雨伞上的效果是一样的.下面就从理想气体的微观模型出发，应用力学规律和统计方法，导出平衡态下理想气体的压强公式.

如图7.2 所示，边长分别为L1、L2、L3 的长立方体容器中，有N个同种气体分子，分子质量为m.将气体分子从1 到N 进行编号，计算N 个分子在垂直于x 轴的器壁A1 面上的压强.

对单个气体分子运用力学规律，计算其对器壁的作用，然后应用统计规律计算大量气体分子的集体作用效果，导出系统的压强公式.

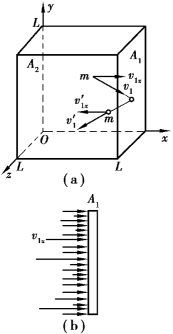
图7.2　理想气体压强

首先考虑编号为i 的分子与器壁A1 碰撞一次施于器壁A1 的冲量：

设第i 个分子的速度为vi=vixi+viy j+vizk，当其与器壁作完全弹性碰撞时，受到器壁给予它的垂直于A1 面的作用力，碰后其速度变为根据动量定理，该气体分子受到器壁的冲量为

根据动量定理及牛顿第三定律，器壁受到气体分子的冲量大小为2mvix，方向指向器壁.

然后计算编号为i 的分子在单位时间内施于器壁A1 的冲量：

为简单起见，设分子在运动过程中不与其他气体分子相碰撞.在运动中，分子虽与其他器壁侧面的内壁相碰，但并不会改变它在x 方向上的运动速度.分子在x 方向上的运动就像在相距为L1的两个平面间作匀速率的折返跑一样.因此，容易算出第i 个分子在单位时间内与A1 面碰撞的次数为则它在单位时间内施于器壁A1 的冲量为

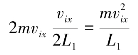
接下来计算器壁内的N 个气体分子在单位时间内施于器壁A1 的冲量：(www.xing528.com)

器壁内的所有分子都可能与器壁A1 相碰.N 个气体分子在单位时间内施于器壁A1 的冲量等于各个分子在单位时间内施于A1的冲量的和，设为I，则

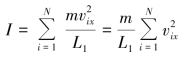
根据力学中平均冲力的概念，若在Δt 时间内，力的冲量为I，则平均冲力它在数值上等于单位时间内力的冲量.而压强等于单位面积上的压力.因此，气体分子在单位时间内施于单位面积器壁的冲量即为压强，因此可得A1 面上的压强为

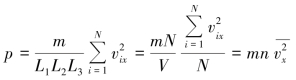
式中，为N 个气体分子在x 方向上分速度平方的平均值；n=为分子数密度.

处于平衡态时，每个分子沿各个方向运动的概率是相等的，没有哪个方向占有优势.因此对大量分子来说，它们在x、y、z 三个轴上的速度分量的平均值应是相等的.即

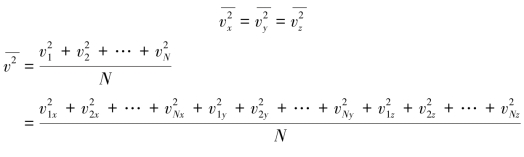
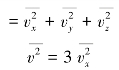
可得理想气体压强公式为

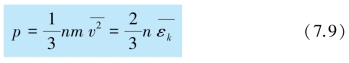
式中，为气体分子的平均平动动能.

由式（7.9）可知，压强p 是描述气体状态的宏观物理量，而分子平均平动动能则是微观量的统计平均值，单位体积内的分子数n 也是统计平均值.因此压强公式反映了宏观量与微观量统计平均值之间的关系，压强的微观意义是大量气体分子在单位时间内施于器壁单位面积上的平均冲量.离开了大量和平均的概念，压强就失去了意义，对单个分子谈不上压强这个物理量.