波动能量与波源振动及介质形变的关系

在波动传播过程中，波源的振动通过弹性介质由近及远地传播出去，使介质中各个质点依次在各自的平衡位置附近振动，因此具有动能，同时该处的介质也发生弹性形变，因此也具有了势能.此能量显然来自波源.可见，波动过程也是能量的传播过程，这是波动的重要特征.

在介质中任取体积为ΔV、质量为Δm=ρΔV（ρ 为介质的体密度）的质量元.如果介质中平面简谐波的波函数为

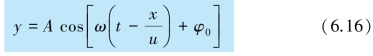
可以证明，当波动传播到该质量元时，这个质量元获得的动能ΔEk 和势能ΔEp 为

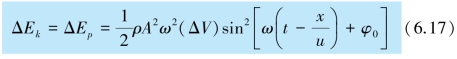
可见，势能与动能的表示式是完全相同的，都是时间的周期函数，并且大小相等，相位相同.这种情况与单个简谐振子完全不同.在波动中与势能相联系的是质量元间的相对位移Δy/Δx.如图6.8 所示，质量元在平衡位置时，速度最大，动能最大，同时波形曲线最陡峭，Δy/Δx 有最大值，该处形变最大，所以弹性势能也最大.质量元处于最大位移处时，速度为零，动能为零，Δy/Δx 也为零，该处无形变，所以弹性势能为零.

进一步我们可以得出质量元获得的总机械能为

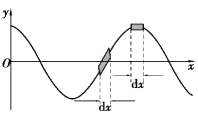
图6.8　势能与质量元间相对位移的关系图(www.xing528.com)

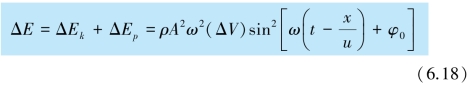
由此可知，在波动过程中，介质中给定质点的总能量不是常量，而是随时间作周期性变化的量.这表明，介质中所有参与波动的质点都在不断地接受来自波源的能量，又不断把能量释放出去，这一点与振动的情况是完全不同的.对于振动系统，总能量是恒定的，不传播能量.振动能量的辐射，实际上是依靠波动传播出去的.

介质中单位体积的波动能量，称为波的能量密度，用w 表示，即

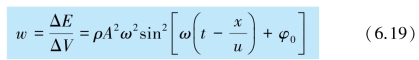
上式表明，波的能量密度是随时间作周期性变化的，通常取其在一个周期内的平均值，这个平均值称为平均能量密度，可以表示为

上式表明，波的平均能量密度与振幅的平方、频率的平方和介质密度的乘积成正比.这个公式虽然是从平面简谐波的特殊情况导出的，但是对于所有机械波都适用.