大学物理学平面简谐波波函数

一般情况下的波是很复杂的，下面只讨论一种最简单、最基本的波，即在均匀、无能量吸收的介质中，当波源作简谐振动时，在介质中所形成的波.这种波称为简谐波.如果简谐波的波面是平面，则这样的波称为平面简谐波.平面简谐波传播时，在任一时刻处在同一波面上的各点具有相同的振动状态.因此，只要知道了与波面垂直的任意一条波线上波的传播规律，就可以知道整个平面波的传播规律.

严格的简谐波只是一种理想的模型.它不仅具有单一的频率和振幅，而且必须在空间和时间上都是无限延展的.严格的简谐波并不存在.对于做简谐运动的波源在均匀、无能吸收的介质中所形成的波，可近似地看成简谐波.可以证明，任何非简谐的复杂波，都可以看成若干个频率不同的简谐波叠加而成的.因此，研究简谐波具有十分重要的意义.

如图6.4 所示，设在各向同性、无能量吸收的均匀介质中，一列平面简谐波沿x 轴的正方向传播，波速为u.在波线上取一点O 作为坐标原点，该波线就是x 轴.假定O 点处质点的振动方程为

图6.4　振动波形图

式中A 为振幅，ω 为角频率，φ0 为初相位.现在考察波线上另一任意点P 的振动情况，点P 离点O 的距离为x.振动从原点O 传播到点P 所需要的时间为Δt，在这段时间内点O 振动了νΔt 次，每振动一次相位改变2π，所以点O 的振动相位在这段时间内改变了2πνΔt.因为振动是从点O 传播过来的，所以可以说，点P 的振动比点O 的振动落后了2πνΔt 的相位.于是，点P 的相位应为（ωt-2πνΔt），进而点P 的振动方程可写为

考虑代入式（6.9）并将y 的下角标P 省去，则上式变为

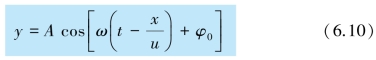
上式表明，波线上任一点（相对原点的距离为x）处的质点的振动方程，也就是沿x 轴的正方向传播的平面简谐波的波函数.

类似上述分析，我们很容易就可以得出沿x 轴的负方向传播的平面简谐波的波函数为

注意：式（6.10）和式（6.11）中的x 应理解为波线上任一点的坐标，应代入坐标的正负号.

下面对波函数的物理意义做以下分析：

（1）如果考察质点P 是确定的，即x 给定，那么y 就只是t 的函数（好似用摄像机对着各特定点连续拍摄）.此时波函数表示距离原点为x 处的质点P 在各个时刻的位移.对应的函数曲线如图6.5 所示，为质点P 的振动曲线.

（2）如果t 是确定的，那么y 就只是x 的函数（好似用照相机对着一组质点在t 时刻拍一张照片）.此时波函数表示在给定时刻波线上各个质点的位移.对应的函数曲线如图6.6 所示，为给定时刻的波形图.

（3）如果x 和t 都在变化，那么此时波函数表示波线上不同质点在不同时刻的位移（好似用摄像机对着一组质点不间断拍摄）.图6.7 分别画出了t 时刻和t+Δt 的两个波形图.

由图6.7 可见，在Δt 时间内，波形曲线沿波的传播方向移动了Δx 的距离.进一步分析，我们可以看出，假定在t 时刻，x 处质点的位移y 经过Δt 的时间出现在了（x+Δx）处，根据式（6.10）有

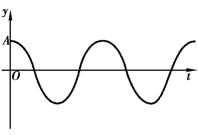
图6.5　考察质点P 的振动曲线

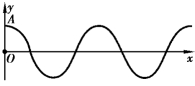
图6.6　给定时刻的波形图

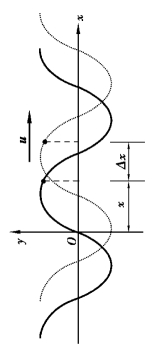
图6.7　不同时刻的波形图

进而得

这表示，振动状态以波速u 沿波的传播方向传播.因此，当x和t 都在变化的时候，这个波函数反映了波形的传播，看起来好像是波形在沿波的传播方向行进，称为行波.

平面简谐波函数还可以表示成以下形式：

(www.xing528.com)

式中称为角波数，表示在2π 米内所包含的完整波的数目.式中负号表示波沿Ox 轴正方向传播，正号表示沿Ox 轴负方向传播.

与谐振动可以用复数表示一样，平面简谐波的波函数也可以用复数来表示

该复数的实部才是平面简谐波的波函数.在量子力学中的波函数一般是复数函数，常用上式的形式表示.

例6.1　频率为ν=12.5 kHz 的平面余弦纵波沿细长的金属棒传播，波速为5.0×103m/s，如以棒上某点取为坐标原点，已知原点处质点振动的振幅为A=0.1 mm，试求：（1）原点处质点的振动表达式；（2）波函数；（3）离原点10 cm 处质点的振动表达式；（4）离原点20 cm和30 cm 两点处质点振动的相位差.

解　

（1）原点处质点的振动表达式为

（2）波函数为

式中x 以m 计，t 以s 计.

（3）离原点10 cm 处质点的振动表达式为

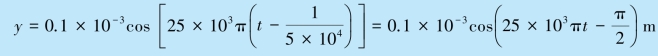
（4）离原点20 cm 和30 cm 两点处质点振动的相位差为

例6.2　频率为3 000 Hz 的声波，以1 560 m/s 的传播速度沿一波线传播，经过波线上的A 点后，再经13 cm 而传到B 点.求：

（1）B 点的振动比A 点落后的时间；

（2）波在A、B 两点振动时相位差是多少？

（3）设波源做简谐运动，振幅为1 mm，求振动速度的幅值，是否与波的传播速度相等？

解　（1）因为波的周期为

波长为

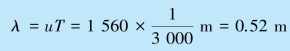
所以B 点的振动比A 点落后的时间为

（2）由于A、B 两点距离相差所以波在A、B 两点振动时的相位差为

（3）如果振幅A=1 mm，则振动速度的幅值为

振动速度随时间按余弦函数形式做周期变化，幅值为18.8 m/s，远小于波动的传播速度1 560 m/s.