两个垂直简谐振动合成|大学物理学（上册）

当质点同时参与两个不同方向的振动时，质点的位移是这两个振动的位移的矢量和.在一般情形下，质点将在平面上做曲线运动，质点的轨道有各种形状.轨道的形状由两个振动的周期、振幅和相位差来决定.

为简单起见，先讨论两个相互垂直的、同频率的简谐振动的合成.

设两个简谐振动分别在x 轴和y 轴上进行，振动表达式分别为

在任一时刻t，质点的位置是（x，y）.t 改变时，（x，y）也改变.由以上两式把参量t 消去，就得到合振动轨迹的直角坐标方程

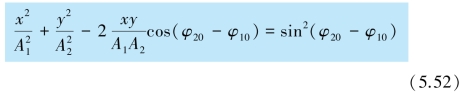
一般地说，上述方程是椭圆方程.因为质点的位移x 和y 在有限范围内变动，所以椭圆轨道不会超出以2A1 和2A2 为边的矩形范围.椭圆的性质（即长短轴的大小和方位），由相位差（φ20-φ10）来决定.下面分析几种特殊情形：

（1）φ20-φ10=0，即两振动同相.在这种情况下，式（5.52）变为

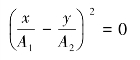
即

质点的轨道是一条直线.这直线通过坐标原点，斜率为这两个振动振幅之比如图5.12（a）所示.在任一时刻t，质点离开平衡位置的位移

所以合运动也是谐振动，周期等于原来的周期，振幅为

如果两个振动的相位差为φ20-φ10=π，即两振动反相，则质点在另一条直线上作同频率的谐振动，其振幅也等于A=如图5.12（b）所示.

（2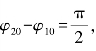）在这种情况下，式（5.52）变为(www.xing528.com)

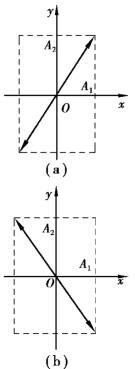
图5.12　合振动情况一

即质点运动的轨道是以坐标轴为主轴的椭圆，振动沿顺时针方向进行，如图5.13 所示.如果这时运动方向与上例相反.

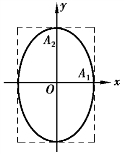
图5.13　合振动情况二

当两个等幅（A1=A2）的振动相位差为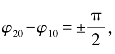椭圆将变为圆.

总之，两个相互垂直的同频率简谐振动合成时，合运动的轨道是椭圆.椭圆的性质视两个振动的相位差而定.

以上讨论也说明：一个沿直线的简谐振动、匀速圆周运动和某些椭圆运动都可以分解成为两个相互垂直的简谐振动.

现在来讨论两个相互垂直但具有不同频率的简谐振动的合成.如果两个振动的频率有很小差异，相位差就不是定值，合运动的轨道将不断地按照图5.14 所示的顺序在上述的矩形范围内由直线逐渐变成椭圆，又由椭圆逐渐变成直线，并重复进行.

如果两个振动的频率相差很大，但有简单的整数比值的关系，也可得到稳定的封闭的合成运动轨道.图5.14 表示两个相互垂直、具有不同频率比的简谐振动的合成的几个简单例子.两振动的频率为其他比值的类似曲线，种类很多，这里不一一绘出.这些曲线称为利萨如图形.利用这些图形，可由一已知频率求得另一个振动的未知频率；若频率比已知，则可利用这种图形确定相位关系，这是无线电技术中常用的测定频率、确定相位关系的方法.

如果两个互相垂直的简谐振动的频率之比为无理数，那么合振动的轨迹将不重复地扫过整个所限定的矩形范围.这种非周期性运动称为准周期运动.

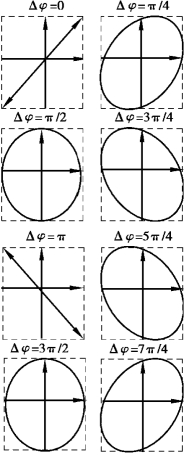
图5.14　两个相互垂直的同频率简谐运动

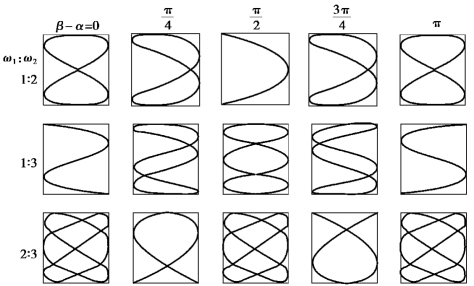
图5.15　利萨如图形