振动合成：相同方向近频简谐振动【大学物理学】

设某物体同时参与了两个振动方向（如x 轴）相同、频率相近的简谐振动，以物体的平衡位置为原点，在任一时刻这两个振动可以分别表示为

与上一种情况相同，物体所参与的合振动就一定也处于这同一条直线上，合位移应等于两个分位移的代数和，即

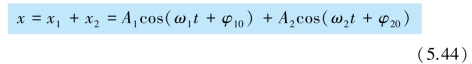
但是与上一种情况不同的是，这时的合振动不再是简谐振动，而是一种复杂的振动.

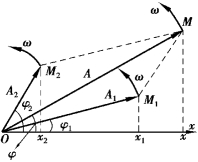
图5.10　两个同方向、同频率简谐运动合成的旋转矢量图

我们用简谐振动的矢量图解法看一下这种振动的大致情况.如图5.10 所示，两个分振动分别对应于旋转矢量A1 和A2.由于这两个旋转矢量绕点O 转动的角速度不同，所以它们之间的夹角随时间而变化.假如在某一瞬间，旋转矢量A1、A2 和它们的合矢量A′处于图5.10 中所示位置，而在以后的某一瞬间，旋转矢量A1 和A2 分别达到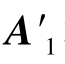和的位置，它们的合矢量变为A′.在这两个任意时刻，由于两个分振动所对应的旋转矢量的夹角不同，合矢量A 和A′的长度也不同，所以，合振动的振幅不再是定值，而是随时间变化.

在t 时刻，旋转矢量A1 和A2 之间的夹角为[（ω2-ω1）t+（φ20-φ10）]，合矢量A 的长度即为合振动的振幅，可以表示为

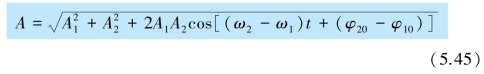
由上式可见，合振动的振幅随时间在最大值A1+A2 和最小值之间变化.

如果ω2>ω1，或者分振动的频率ν2>ν1，那么每秒钟旋转矢量A2 绕点O 转ν2 圈，旋转矢量A1 绕点O 转ν1 圈，A2 比A1 多转（ν2-ν1）圈.A2 比A1 多转一圈，就会出现一次两者方向相同的机会和一次方向相反的机会，所以在1 s 内应出现（ν2-ν1）次同方向的机会和（ν2-ν1）次反方向的机会.两者同方向时，合振动的振幅为A1+A2；两者反方向时，合振动的振幅为.这样，当两个分振动的频率存在微小差异时就形成了合振动振幅时而加强、时而减弱的所谓的拍现象.合振动在一秒内加强或减弱的次数称为拍频，存在关系

另外还可以利用三角函数运算求拍频.为简便起见，假定两个简谐振动的振幅和初相位分别相同，为A 和φ0，则式（5.44）可整理成(www.xing528.com)

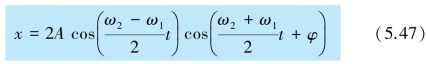
在上式中，当ω1 和ω2 相差很小时，（ω2-ω1）比ω1 和ω2 都小得多，因而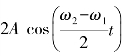是随时间缓慢变化的量，可以把它的绝对值看作合振动的振幅.此合振动的振幅是时间的周期性函数.由于余弦函数的绝对值以π 为周期，即存在

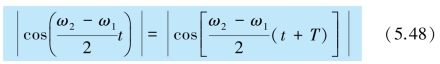
进而有

所以，振幅的周期是

故拍频为

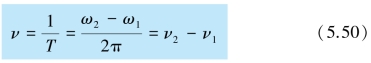
图5.11 为两个分振动及合振动的图形.

拍现象可以通过如下演示实验验证.取两个频率相同的音叉，在其中一个音叉上套上一个小铁圈或粘贴上一块橡皮泥，使这个音叉的频率发生很小的改变.当同时敲击这两个音叉时，除了音叉的振声以外，还会听到另一种“嗡嗡嗡……”的声音，反映出合振动的振幅存在时强时弱的周期性变化，这就是拍的现象.

拍现象在技术上有重要应用.例如，管乐器中的双簧管就是利用两个簧片振动频率的微小差别产生颤动的拍音；调整乐器时，使它和标准音叉出现的拍现象消失来校准乐器.拍现象还可以用来测量频率：如果已知一个高频振动频率，使它和另一频率相近但未知的振动叠加，测量合成振动的拍频，就可以求出未知的频率.超外差收音机是利用拍现象的另一个典型例子，它将被接收信号与本机振荡所产生的拍频信号进行放大、检波，从而提高整机灵敏度.拍现象常用于汽车速度监视器、地面卫星跟踪等.此外，在各种电子学测量仪器中，也常常用到拍现象.

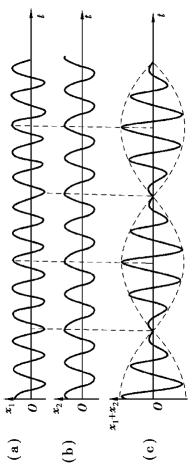
图5.11　两个分振动及合振动的图形