振动方向相同的两个同频率简谐振动的合成

设一物体同时参与了两个振动方向（如x 轴）和频率都相同的简谐振动.以物体的平衡位置为原点，在任一时刻，这两个振动可以分别表示为

既然两个简谐振动处于同一条直线上，可以认为x1 和x2 是相对同一平衡位置的位移，于是，物体所参与的合振动就一定也处于这同一条直线上，合位移应等于两个分位移的代数和，即

根据简谐振动的旋转矢量图解法，可以求出物体所参与的合振动.如图5.8 所示，两个振动的合成反映在矢量图上应该是两个旋转矢量的合成.所以，合成的振动应该是矢量A1 和A2 的合矢量A 的末端在x 轴上的投影点沿x 轴的振动.因为矢量A1 和A2 都以角速度ω 绕点作逆时针旋转，因此它们的夹角是不变的，始终等于（φ20-φ10），则合矢量A 的长度也必定是恒定的，并以同样的角速度ω 绕点O 作逆时针旋转.

合振动的振幅为

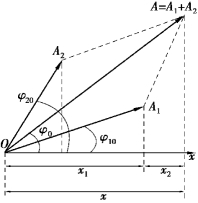
图5.8　同一直线上两个同频率的谐振动合成的矢量图

合振动的初相位为

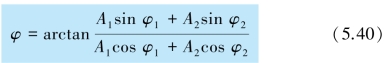
下面根据相位差不同，讨论两种特殊情况：

（1）如果分振动的相位差φ20-φ10=±2kπ，k=0，1，2，…，那么从式（5.39）可得

这表示，当两个分振动相位相等或相位差为π 的偶数倍时，合振动的振幅等于两个分振动的振幅之和，这种情形称为振动互相加强，如图5.9（a）所示.

（2）如果分振动的相位差φ20-φ10=±（2k+1）π，k=0，1，2，…，那么从式（5.39）可得(www.xing528.com)

这表示，当两个分振动相位相反或相位差为π 的奇数倍时，合振动的振幅等于两个分振动振幅之差的绝对值，这种情形称为振动互相减弱，如图5.9（b）所示.如果A1=A2，则A=0，即振动合成的结果使物体处于静止状态.

在一般情况下，相位差（φ20-φ10）不一定是π 的整数倍，合振动的振幅则处于A1+A2 和之间的某一确定值.

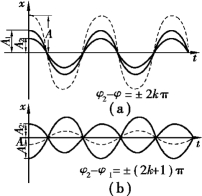
图5.9　振动互相加强

上述结果表明，两个振动的相位差对合振动起着重要作用.

例5.3　一个质点同时参与两个同方向同频率的简谐运动，其振动方程分别为

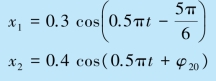
试问：

（1）φ20为何值时合振动的振幅最大？其值为多少？

（2）若合振动的初相位则φ20为何值？合振动的振幅为多少？

解　（1）当两个振动同相时，合振动的振幅最大，即此时，合振动的振幅为

（2）根据旋转矢量图解法可知，只有当时，合振动的初相位才为此时，合振动的振幅为