大学物理学上册：5种简谐振动详解

1）单摆

一根不可伸缩的轻质细线，上端固定（或一根刚性轻杆，上端与无摩擦的铰链相连），下端悬挂一个很小的重物，把重物略加移动后就可在竖直平面内来回摆动，这种装置称为单摆，如图5.5 所示.静止时，细线沿竖直方向，物体处于点O.此时，作用在重物上的合外力为零，位置O 即为振动系统的平衡位置.

设在某一时刻，单摆的摆线偏离沿垂线的角位移为θ，并规定摆锤在平衡位置的右方时，θ 为正；在左方时，θ 为负.若悬线长为l，则重力G 对点A 的力矩为M=-mgl sin θ，负号表示力矩方向与角位移θ 的方向相反.拉力FT 对该点的力矩为零.当角位移θ 很小时（小于5°），sin θ≈θ，则摆锤所受的力矩为

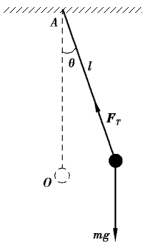
图5.5　单摆模型

式中M 与θ 的关系，恰似弹性力F 与位移x 的关系.根据转动定律单摆的角加速度为

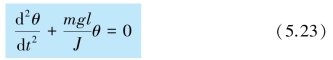
式中J 为摆锤对悬挂点A 的转动惯量（J=ml2）.因此，上式可写成

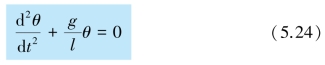
上式表明，在θ 很小时，单摆的角加速度与角位移成正比但方向相反，这与式（5.4）的形式完全相同.可见，单摆的运动具有简谐运动的特征，因而也是简谐运动.

把式（5.24）与式（5.4）比较可知，单摆在摆角很小时，在平衡位置附近作角谐振动，其角频率和周期分别为

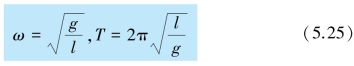
其振动表达式为

θm 是最大角位移，即角振幅，φ0 为初相位，它们均由初始条件决定.

在单摆中，物体所受的回复力不是弹性力，而是重力的切向分力.在θ 很小时，此力与角位移θ 成正比，方向指向平衡位置，虽然本质上不是弹性力，但其作用完全与弹性力一样，所以是一种准弹性力.(www.xing528.com)

当θ 不是很小时，物体所受的回复力与sin θ 成正比，物体不再做谐振动.由于sin θ 总是小于θ，所以，当摆动幅角较大时，单摆的振动周期将增大，单摆的周期T 与角振幅θm 的关系为

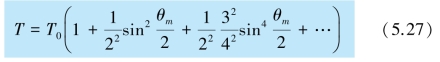
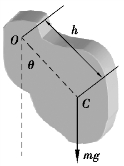
图5.6　复摆模型

2）复摆

如图5.6 所示，一个可绕固定轴摆动的刚体称为复摆，也称物理摆.平衡时，摆的重心在轴O 的正下方.摆动时，重心与轴的连线偏离平衡时的竖直位置.设在任一时刻t，其间的夹角为θ.规定：重心处于平衡位置右方时对应的角位移为正.此时，复摆受到的对于O 轴的力矩为

式中负号表示力矩与角位移的方向相反，h 为重心C 到转轴O 的距离.

当摆角很小时，有sin θ≈θ，则上式变为M=-mghθ，根据转动定律，得

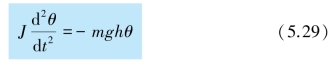
整理得

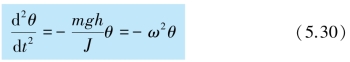
式中J 为复摆对转轴O 的转动惯量.上式与式（5.4）相比较，可知复摆在摆角很小的情况下也在其平衡位置附近作简谐振动，其周期为

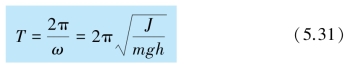
上式表明复摆的周期也完全决定于振动系统本身的性质.由上式可知，如果测出复摆的质量m，重心到转轴的距离h，以及复摆的周期T，就可以求得此复摆绕该轴的转动惯量.有些形状复杂物体的转动惯量，用数学方法进行计算比较困难，有时甚至是不可能的，但用上述的振动方法就可以测定.