简谐振动可以用一个旋转矢量来描绘.如图5.3 所示,在平面内画坐标轴Ox,由原点O 作一个矢量![]() 矢量的长度等于振幅A,规定该矢量以数值等于角频率ω 的角速度在平面内绕O 点做逆时针方向的匀速转动,这个矢量称为振幅矢量,用A 表示.设在t=0 时,振幅矢量A 与Ox 轴之间的夹角为φ0,等于简谐振动的初相位.经过时间t,振幅矢量A 转过角度ωt,与Ox 轴之间的夹角变为(ωt+φ0),等于简谐振动在该时刻的相位.这时振幅矢量A 的末端在Ox 轴上的投影点P 的位移是
矢量的长度等于振幅A,规定该矢量以数值等于角频率ω 的角速度在平面内绕O 点做逆时针方向的匀速转动,这个矢量称为振幅矢量,用A 表示.设在t=0 时,振幅矢量A 与Ox 轴之间的夹角为φ0,等于简谐振动的初相位.经过时间t,振幅矢量A 转过角度ωt,与Ox 轴之间的夹角变为(ωt+φ0),等于简谐振动在该时刻的相位.这时振幅矢量A 的末端在Ox 轴上的投影点P 的位移是
![]()
这正是简谐振动的表达式.可见,做匀速转动的矢量A,其端点M在Ox 轴上的投影点P 的运动是简谐振动.在矢量A 的转动过程中,M 点作匀速圆周运动,通常把这个圆称为参考圆.矢量A 转一周所需的时间就是简谐振动的周期.
由此可见,简谐振动的旋转矢量表示法把描述简谐振动的三个特征量非常直观地表示出来了.这种图示法的依据是充分利用匀速圆周运动是周期性运动的特性.该方法在电学和光学中都有应用.
利用旋转矢量可以比较两个同频率简谐运动的“步调”如何.设有下列两个简谐运动:

图5.3 简谐振动的
旋转矢量图解法
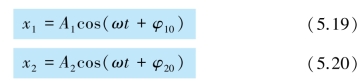
它们之间的相位差用Δφ 表示:
![]()
即两个同频率的简谐运动在任意时刻的相位差,都等于其初相位差.
如果Δφ=φ20-φ10>0,我们就说x2 振动超前x1 振动Δφ 相位,或者说x1 振动落后x2 振动Δφ 相位.如果Δφ=0(或者2π 的整数倍),我们就说这两个振动是同相的,即它们将同时到达正最大位移处,同时到达平衡位置,又同时到达负最大位移处,两个振动的“步调”完全一致.如果Δφ=π(或者π 的奇数倍),就说这两个振动是反相的,两个振动的“步调”完全相反.
例5.1 有一弹簧振子按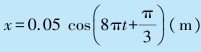 的规律振动,式中t 以s 为单位,x以m 为单位.试求:
的规律振动,式中t 以s 为单位,x以m 为单位.试求:
(1)振动的角频率、周期、振幅、初相位、速度及加速度的最大值;
(2)t=1 s,t=5 s 等时刻的相位;
解 根据题意可知,该弹簧振子作简谐振动.将题中给出的运动学方程与谐振动的一般形式
![]()
作比较可得
![]()
振动的速度为
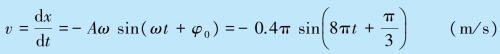
速度的最大值为
![]()
振动的加速度为(https://www.xing528.com)

速度的最大值为
![]()
(2)t=1 s 时的相位为![]()
t=5 s 时的相位为φ![]()
例5.2 一振动质点的振动曲线如图5.4 所示,试求:
(1)运动学方程;
(2)点P 对应的相位;
(3)从振动开始到达点P 相应位置所需的时间.
解 设质点振动的运动学方程为

图5.4 例5.2 用图
![]()
据题图可知,A=0.10 m,![]()
根据旋转矢量图解法,得
![]()
据题图可知,t=1 s 时,x1=0,有 可得
可得
![]()
所以,该质点振动的运动学方程为
![]()
(2)根据该质点振动的运动学方程以及题图,可知点P 对应的相位为零.
(3)从振动开始到达点P 相应位置所需的时间为
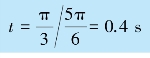
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




