大学物理学：描述简谐振动特征量

振幅、周期（或频率）和相位是描述简谐振动的三个重要物理量，若知道了某简谐振动的这三个量，该简谐振动就完全被确定了，故称描述简谐振动的特征量.

1）振幅

在简谐振动表达式中，因余弦（或正弦）函数的绝对值小于或等于1 ，所以物体的振动范围在+A 和-A 之间，于是将简谐振动的物体离开平衡位置的最大位移的绝对值A 叫做振幅.

2）周期和频率

振动的特征之一是运动具有周期性，将振动物体完成一次完整振动所经历的时间称为周期，用T 来表示.因此，每隔一个周期，振动状态就完全重复一次，即

比较可得

则弹簧振子的周期为

单位时间内物体所做的完全振动的次数叫做频率，用希腊字母ν 表示，单位是赫兹，符号为Hz.频率与周期的关系为

由上式可知

即ω 等于物体在单位时间内所做的完全振动次数的2π 倍，称为角频率（又称圆频率），单位是rad·s-1（弧度每秒）.

由于弹簧振子的角频率是由弹簧振子的质量和劲度系数所决定的，所以周期和频率只和振动系统本身的物理性质有关.这种只由振动系统本身的固有属性所决定的周期和频率，叫做振动的固有周期和固有频率.周期和频率是反映物体周期性运动特征的物理量.(www.xing528.com)

3）相位

相，有状态的意思，相位就是所处的状态.由式（5.6）可知，弹簧振子的运动状态由（ωt+φ0）决定，（ωt+φ0）称为简谐振动的相位，φ0 是t=0 时的相位，称为初相位.相位的单位是rad（弧度）.在角频率ω 和振幅A 已知的谐振动中，振动物体在任一时刻t 的运动状态（指位置和速度）都由相位（ωt+φ0）决定.由下面的分析可清楚地表明这一点.将式两边对时间求一阶导数，可以得到物体振动的速度

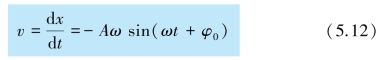
由式（5.6）和式（5.12）可以看出，在角频率ω 和振幅A 已知的谐振动中，振动物体在任一时刻t 的位置和速度完全由相位（ωt+φ0）决定.物体的振动，在一个周期内，每一时刻的运动状态都不相同，这相当于相位经历着从0 到2π 的变化.凡是位移和速度都相同的运动状态，它们所对应的相位相差为0 或2π 的整数倍.由此可见，相位也能反映周期性的特点，是描述物体运动状态的重要物理量.

相位概念的重要性还在于比较两个谐振动之间在“步调”上的差异.设有两个同频率的谐振动，它们的振动表达式为

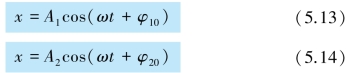
它们的相位差为

即它们在任意时刻的相位差都等于它们的初相位差.当Δφ等于0 或2π 的整数倍时，这时两振动物体将同时到达各自同方向的位移的最大值，同时通过平衡位置而且向同方向运动，它们的步调完全相同，称这样的两个振动为同相.当Δφ 等于π 或π 的奇数倍时，则一个物体到达正的最大位移时，另一个物体到达负的最大位移处，它们同时通过平衡位置但向相反方向运动，即两个振动的步调完全相反，称这样的两个振动为反相.

当Δφ 为其他值时，如果φ20-φ10>0，称第二个简谐振动超前第一个振动Δφ，或者说第一个振动落后于第二个振动Δφ.图5.2画出了两个同频率、同振幅、不同初相的简谐振动的位移时间曲线.两简谐振动具有恒定的相位差（φ20-φ10），它们的变化在步调上相差一段时间

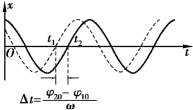
图5.2　两个同振幅、同频率而不同初相位的谐振动的位移时间曲线

相位还可以比较不同物理量变化的步调.例如，比较物体作谐振动时的速度、加速度和位移变化的步调，其中速度和加速度的表达式可以写为

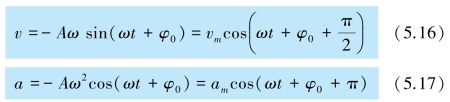
可以看出，除它们的幅值不同外，速度的相位比位移的相位超前加速度比位移的相位超前π，也就是两者是反相的.