由式(4.21)可以看出,当刚体所受外力对转轴的合力矩为零时,即Mz=0,可得
![]()
这就是说,当定轴转动的刚体所受外力对转轴的合力矩为零时,刚体对同一转轴的角动量不随时间变化.这个结论称为刚体对转轴的角动量守恒定律.
当定轴转动系统由多个物体组成(如刚体组)时,角动量守恒定律仍然成立.例如由两个物体组成的转动系统,当系统所受外力对转轴的合力矩为零时,即Mz=0,可得
![]()
亦即当系统内一个物体的角动量发生了变化,则另一个物体的角动量必然有个与之等值异号的改变,从而使总角动量保持不变.
有许多现象都可以用角动量守恒定律来说明.如图4.7 所示,人手持哑铃坐在可绕竖直轴转动的凳上,开始时人将双臂伸开,并使人和凳以一定角速度转动.当人将双臂收拢,哑铃移到胸前时,转动惯量减小,人和凳的转动角速度会显著增大.若人重新将双臂伸开,转动惯量增大,人和凳的转动角速度又会减小了.
芭蕾舞演员和花样滑冰运动员,在做各种快速旋转动作时,也是利用了对转轴的角动量守恒定律的.开始他们总是先将臂、腿伸展开,以一定的角速度旋转,然后突然将臂、腿收拢,使转动惯量减小,转速则立即增大了.
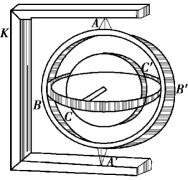
刚体对转轴的角动量守恒定律在现代科学技术中也有重要应用.图4.8 是一个装在常平架上的回转仪(也称陀螺仪).常平架是由支撑在框架K 上的两个圆环组成,两圆环可分别绕其支点A、A′和B、B′所确定的轴自由转动.回转仪是一个具有较大转动惯量,并可绕安装在内环上的轴CC′高速旋转的厚重、对称的转子.AA′、BB′和CC′三轴互相垂直,并且都通过回转仪的重心.当回转仪以高速旋转时,因为不受任何外力矩的作用,其转轴CC′在空间的取向将恒定不变.如果将这种装置安放在舰船、飞机或导弹上,与自控系统配合,可以随时矫正运行的方向,起导航作用.
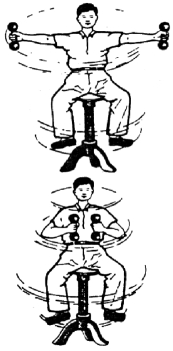
图4.7 角动量守恒现象
 (https://www.xing528.com)
(https://www.xing528.com)
图4.8 回转仪
例4.5 工程上,常用摩擦啮合器使两飞轮以相同的转速一起转动.如图4.9 所示,A和B 两飞轮的轴杆在同一中心线上,A 轮的转动惯量为JA=10 kg·m2,B 轮的转动惯量为JB=20 kg·m2.开始时A 轮的转速为600 r/min,B 轮静止.C 为摩擦啮合器.求两轮啮合后的转速.在啮合过程中,两轮的机械能有何变化?

图4.9 例4.5 用图
解 将两飞轮和啮合器作为一系统来考虑.在啮合过程中,系统受到轴向的正压力和啮合器间的切向摩擦力,前者对转轴的力矩为零,后者对转轴有力矩,但为系统的内力矩.可见系统的角动量守恒,满足
![]()
ω 为两轮啮合后共同转动的角速度,于是有

或共同转速为 n=200 r/min
在啮合过程中,摩擦力矩做功,所以机械能不守恒,部分机械能将转化为热量.损失的机械能为
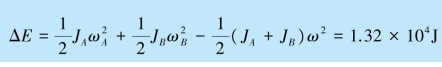
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




