在质点力学中，如果质点在外力作用下沿力的方向发生位移，那么力就对质点做了功.在刚体转动时，作用力可以作用在刚体的不同质点上，各个质点的位移也不相同.只要将各个力对相应质点做的功加起来，就能求得力对刚体所做的功.由于在转动的研究中，使用角量比使用线量方便，因此在功的表达式中以力矩的形式出现，力做的功也就是力矩的功.
对定轴转动的刚体起作用的力矩，只有力矩沿转轴的分量，即若取转轴为z 轴，则起作用的只有Mz，而Mz 又只是由F 在Oxy 平面（或任意一个转动平面）内的投影分量产生.所以在讨论刚体定轴转动时，只需考虑外力F 在Oxy 平面内的分力就可以了.为方便讨论，约定以下所提及的外力都只是处于转动平面内的力.
假定作用于以z 轴为转轴的刚体上的多个外力分别为F1，F2，…，Fn.先考虑其中的任一外力Fi 对刚体的作用.如图4.4 所示，外力Fi 作用于刚体上的点P，过点P 作垂直于z 轴的平面，交z 轴于点O，显然这个平面是刚体的一个转动平面.在此平面内，点P 相对于点O 的位置矢量为ri，ri 与Fi 的夹角为φi.在dt 时间内，刚体转过了dθ 角度，点P 对应的位移为dri.在此过程中，外力Fi所做的元功为
式中dsi=ridθ，为点P 在dt 时间内通过的路程.αi 为Fi 与dri 的夹角，满足cos αi=sin φi.Mzi为Fi 对转轴Oz 的力矩.
对于作用于刚体的其他外力，同样也可用上述方法进行分析，并得出与上式相似的结果.因此，在刚体转过dθ 角度的过程中，所有外力做的总功为
图4.4 力矩的功
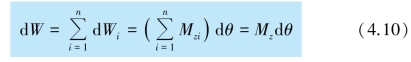
式中
是作用于刚体的所有外力对Oz 轴的合力矩.
如果刚体在力矩Mz 的作用下绕Oz 轴从位置θ1 到θ2，那么，在此过程中力矩所做的总功为(www.xing528.com)
力矩的瞬时功率可以表示为
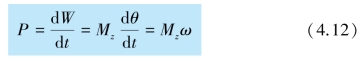
式中ω 为刚体绕轴转动的角速度.
根据质点系的功能原理，外力和非保守内力对系统所做的功等于系统机械能的增量.这一原理对于刚体这一特殊质点系也是适用的.由于一切内力对刚体所做的功为零，所以与定轴转动刚体相对应的关系式为
式中dW 为外力所做的元功，机械能表现为刚体的转动动能.代入刚体转动动能的具体形式，并积分，可得
上式表明，对于定轴转动的刚体，外力矩所做的功等于刚体转动动能的增量.该结论称为定轴转动刚体的动能定理.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
