大学物理学（上册）：刚体转动惯量

从式（4.4）可以看出，刚体相对于某转轴的转动惯量，是组成刚体的各体元质量与它们各自到该转轴距离平方的乘积之和.刚体的质量是连续分布的，式中的求和号应该用积分号来代替，于是有

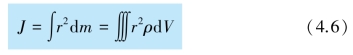
式中的dV 和ρ 分别是体元的体积和密度，r 是该体元到转轴的距离.在国际单位制中，转动惯量的单位是kg·m2（千克·米2）.

虽然上式是计算转动惯量的通式，但只有当刚体的几何形状简单、质量连续且均匀分布时才可较为简便地利用上式计算转动惯量.表4.1 给出了常见刚体的转动惯量.通常情况下，刚体的转动惯量由实验方法测定.

表4.1　几种常见刚体的转动惯量

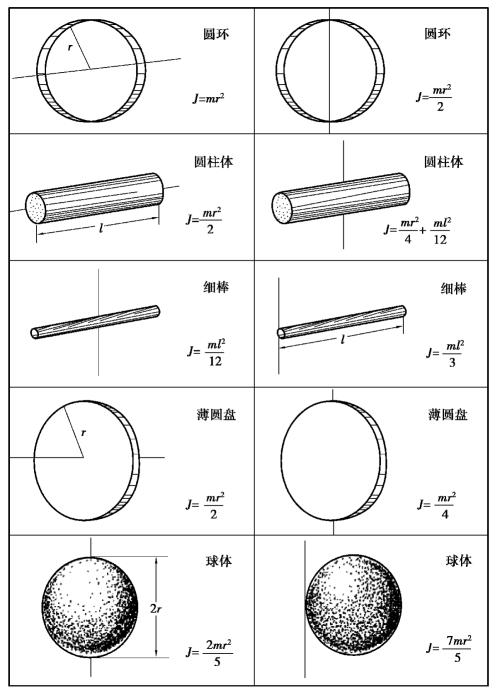
由式（4.6）可知，决定刚体转动惯量大小的因素有三个：

（1）刚体的质量.形状、大小都相同的刚体，质量较大的转动惯量更大.

（2）质量的分布.质量和密度都相同的刚体，质量分布的距离转轴越远（即刚体的形状）不同，转动惯量越大.

（3）转轴的位置.转轴的位置不同，刚体的转动惯量也不同.

下面介绍两个有助于计算刚体转动惯量的定理.

1）平行轴定理

如果刚体对通过质心的轴的转动惯量为JC，那么对与此轴平行的任意轴的转动惯量可以表示为

式中m 是刚体的质量，d 是两平行轴之间的距离.由该定理可知，在刚体对各平行轴的转动惯量中，以对过质心轴的转动惯量为最小.

2）垂直轴定理

若z 轴垂直于厚度为无限小的刚体薄板，xy 平面与板面重合，则此刚体薄板对三个坐标轴的转动惯量有如下关系：

值得注意的是，该定理只适用于厚度非常小的板.(www.xing528.com)

例4.1　一根长为l、质量为m 的均匀细棒，求对下面两种转轴的转动惯量：（1）转轴通过棒的中心并与棒垂直；（2）转轴通过棒的一端并和棒垂直.

解　（1）将棒的中点取为坐标原点，建立坐标系Oxy，取y 轴为转轴，如图4.2 所示.在距离转轴为x 处取线元dx，其质量为

根据式（4.6），应有

图4.2　例4.1 用图

（2）转轴通过棒的一端并和棒垂直时，代入平行轴定理的表达式（4.7）中，得

例4.2　求质量为m、半径为R 的均质薄圆盘对通过盘心并处于盘面内的轴的转动惯量.

解　先根据式（4.6）求出薄圆盘对通过盘心并垂直于盘面的Oz 轴的转动惯量Jz.因为盘的质量分布均匀，所以盘的质量面密度为常量.将圆盘划分成许多圆环，其中任一圆环的半径为r、宽为dr，如图4.3 所示，此圆环的质量为dm=σ2πrdr.则有

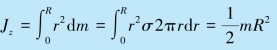
根据垂直轴定理的公式（4.8），有

由于对称性，Jx=Jy，所以薄圆盘对通过盘心并处于盘面内的轴的转动惯量为

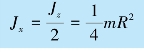
图4.3　例4.2 用图