物体机械运动的基本形式除了平动外,还有转动.实际上,大到星云、星系,小至微观粒子,无不参与转动这一运动形式.角动量则是反映转动规律的重要而又基本的物理量.一个质点或质点系若受到外力作用,可以用动量的时间变化率与外力联系起来,如果所受合外力为零,则动量守恒.与此类似,一个质点或质点系若受到外力矩作用,可以用角动量的时间变化率与外力矩联系起来.如果所受外力矩为零,则角动量守恒.角动量守恒定律是力学中三个守恒定律之一,与动量守恒定律和能量守恒定律一起,构筑了经典力学的基石.其应用范围也已超出了经典力学,对研究宇宙中天体的运动和微观粒子的运动都具有重要意义.
1)力矩
一个静止的物体受到外力作用时,将开始运动,但不一定会转动;只有当外力产生力矩时,物体才能转动.力矩是全面考虑力的三要素的一个重要概念.下面先从一般意义来介绍力矩.
一般来说,力矩是对某一参考点而言的.如图3.14 所示,如果质点P 在坐标系Oxyz 中的位置矢量是r,那么作用于质点的力F相对于参考点O所产生的力矩就定义为
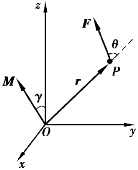
图3.14 力的力矩
![]()
M 的方向由右手定则确定:右手的四指由r 的方向经小于π 的角转向F 的方向,伸直的拇指所指的方向就是力矩M 的方向.
M 的大小为:
![]()
式中θ 为r 与F 之间小于π 的夹角.由于力矩与r 有关,所以,对于同样的作用力F,选择不同的参考点,力矩的大小和方向一般都会不同.为此,一般在作图时可把力矩画在参考点上,而不画在质点上.
如果作用于质点上的力是多个力的合力,即
![]()
代入式(3.44)中,得
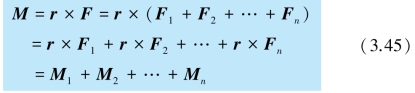
上式表明,合力对某参考点的力矩等于各分力对同一点力矩的矢量和.
在国际单位制中,力矩的单位是N·m(牛·米).
日常所见到的转动很多是绕某固定转轴进行的,如门绕门轴的转动,电风扇叶片绕转轴的转动,螺帽绕螺杆的转动等.下面就对力对转轴的力矩作简单介绍.
在上述物体绕固定轴转动的情况下,由于转轴固定,只有外力具有与转轴垂直的分力时,也就是说,只有力矩矢量具有沿转轴的分量时,物体才能绕轴转动.参见图3.15,若把转轴定为z 轴,则只有力矩沿z 轴的分量Mz 对物体绕轴转动起作用.
在以参考点O 为原点的直角坐标系中,将力矩矢量表示为
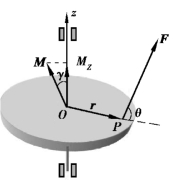
图3.15 绕定轴转动的力矩
![]() (https://www.xing528.com)
(https://www.xing528.com)
其中Mx、My 和Mz 分别是力矩矢量沿三个坐标轴的分量.在同一坐标系中,质点P 的位置矢量和作用力可分别表示为
![]()
将以上两式代入式(3.44)中,即可得到
![]()
对应的分量式为
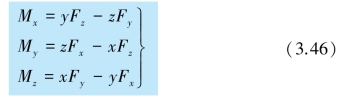
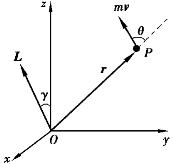
图3.16 角动量
力矩矢量沿某坐标轴的分量通常称为力对该轴的力矩.
利用式(3.46)可以计算力F 对z 轴的力矩Mz.可以证明,对轴的力矩与参考点在轴上的位置无关,也就是说,无论参考点处于轴的什么位置上,只要力F 的大小和方向是确定的,力F 对该轴的力矩就是确定的.
当然,如图3.15 所示,如果知道了力矩的大小和它与z 轴的夹角γ,那么力对z 轴的力矩也可以按下式求得
![]()
2)角动量
前面已经用动量来描述质点和质点系机械运动的状态,并讨论了它们在机械运动过程中所遵循的动量守恒定律.同样,在讨论质点相对于空间某一定点的转动时,也可以用角动量来描述物体的运动状态.
角动量是一个很重要的概念,在转动问题中,它所起的作用和动量相类似.角动量可描述大到天体,小到质子、电子的运动.例如,电子绕核运动,具有轨道角动量,电子自身还有自旋运动,具有自旋角动量等.原子、分子和原子核系统的基本性质之一,只不过它们的角动量仅具有一定的不连续的量值,这叫做角动量的量子化.在这些系统的性质描述中,角动量起着主要作用.
先以一个质量为m 的质点为例阐明角动量的概念.设一个质点位于P 点,相对于参考点O 的位置矢量为r,如图3.16 所示.如果此时质点的速度为v,则这个质点相对于参考点O 的角动量L被定义为
![]()
可见,角动量是一个矢量,它的方向垂直于由矢量r 和p 所决定的平面,其方向由右手定则确定:让右手的四指由矢量r 的方向经小于π 的角转动矢量p 的方向,大拇指所指的方向就是角动量L 的方向.如果位置矢量与动量的夹角为θ,那么角动量的大小由下式决定
![]()
质点对通过参考点的任意轴线的角动量,就是质点相对于同一参考点的角动量沿该轴线的分量.由图3.16 可以看出Lz 为
![]()
在国际单位制中,角动量的单位是kg·m2·s-1.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




