如果两个或几个物体在相遇时,物体之间的相互作用仅持续一个极为短暂的时间,这些现象就是碰撞.碰撞的含义比较广泛,除了各种撞击外,分子、原子、原子核等微观粒子的相互作用过程等也都是碰撞过程,这时粒子间的相互作用是非接触作用.例如分子、原子相互接近时,由于双方很强的相互斥力,迫使它们在接触前就偏离了原来的运动方向而分开,这种碰撞通常称为散射.人从车上跳下,子弹打入墙壁等现象,在一定条件下也可看作碰撞过程.在碰撞过程中,由于相互作用的时间极短,相互作用的冲力又极大,碰撞物体所受的其他作用力相对来说都很小,可以忽略不计.因此,在处理碰撞问题时,常将参与碰撞的物体作为一个系统来考虑,就可以认为系统内仅有内力的相互作用,系统遵从动量守恒定律.下面以两球碰撞为例进行讨论.
如果两球在碰撞前的速度在两球的中心连线上,那么,碰撞后的速度也都在这一直线上,这种碰撞称为正碰撞.设质量为m1和m2 的两球,在碰撞前的速度分别为v10和v20,碰撞后的速度分别为v1 和v2.由动量守恒定律得
![]()
上式中假定碰撞前后各个速度都沿着同一方向.
牛顿从实验结果中总结出了一个碰撞定律:碰撞后两球的分离速度(v2-v1),与碰撞前两球的接近速度(v10-v20)成正比,比值由两球的材料性质决定,即

把e 叫做恢复系数(在斜碰的情况下,式中的分离速度与接近速度都是指沿碰撞接触处法线方向上的相对速度).如果e=1,则分离速度等于接近速度,这称为完全弹性碰撞,是一种理想的情形.一般,用优质钢材、玻璃、象牙等材料制成的小球在碰撞过程中可近似看作弹性碰撞,微观粒子在一定条件下的碰撞则是严格的弹性碰撞,例如低能电子与原子的碰撞等.可以证明,在完全弹性碰撞中,两球的机械能完全没有损失,而在一般情况下,两球在碰撞过程中,机械能并不守恒,总有一部分机械能损失掉,转变为其他形式的能量,例如热力学能等.这种存在机械能损失的碰撞称为非弹性碰撞.如果e=0,则v2=v1,亦即两球碰撞后以同一速度运动,并不分开,称为完全非弹性碰撞.
由式(3.38)、式(3.39)可得

利用上式,讨论如下两类极端情形.
1)完全弹性碰撞
此时e=1,则上式变为

下面分析两种特例:
(1)设m1=m2,代入式(3.41),得
![]()
这时,两球经过碰撞将交换彼此的速度,即速度和能量发生了转移.可见两球的质量越相近,则越接近该种情况.在原子核反应堆中,常用石墨或重水作为中子的减速剂,就是考虑到中子和这些轻原子核(碳原子核或重氢原子核)质量相差不大,碰撞时易于减速的缘故.
(2)设m1≠m2,v20=0,则式(3.41)变为

如果m2≫m1,那么

所以v1≈-v10,v2≈0.可见,质量极大并且静止的物体,经碰撞后,几乎仍静止不动,而质量极小的物体,在碰撞前后的速度方向相反,大小几乎不变,这个现象属于反冲.例如,皮球与地面的碰撞、气体分子与器壁相撞等.(https://www.xing528.com)
2)完全非弹性碰撞
此时e=0,则式(3.40)变为

利用式(3.40)可以计算碰撞过程中损失的机械能,得

由上式可见,在完全非弹性碰撞中,损失的机械能最多.
在工程中,例如打铁、打桩等类问题,经常碰到其中一个物体是静止的.设v20=0,此时损失的机械能为

其中![]() 为碰撞前的机械能,于是上式变为
为碰撞前的机械能,于是上式变为

由此可见,损失的机械能是它原有机械能的一部分,而这部分机械能的大小完全取决于两给定碰撞物体的回复系数和质量比.
在实际问题中,往往根据不同的能量分配要求来选择不同的条件.例如,在打铁时,使铁锤和锻件(连同铁砧)碰撞,要锻件在碰撞过程中发生变形,这时尽量使碰撞中的机械能用于锻件变形,这就要求铁砧的质量比铁锤的质量大得多,即m2≫m1.打桩的情况恰好相反.锤和桩碰撞时,锤把机械能传递给桩,使桩尽可能克服地面的阻力下沉,因此,希望机械能损失得越小越好,这就要求用质量较大的锤撞击质量较小的桩,即m2≪m1.
例3.10 如图3.13 所示,轻弹簧的一端与质量为m2 的物体连接,另一端与一质量可忽略的挡板相连,它们静止在光滑的桌面上.弹簧的劲度系数为k.仅有一质量为m1,速度为v0 的物体向弹簧运动并与挡板发生正面碰撞.求弹簧被压缩的最大距离.
解 设从碰撞开始,到弹簧最大限度地被压缩,最大值为x 时,m1 和m2 以相同速度v运动.该过程是完全非弹性碰撞的过程,m1 和连接弹簧的m2 系统满足动量守恒条件,即
![]()

图3.13 例3.10 用图
在上述过程中,m1 的动能部分转化为弹簧的形变势能.若以m1、m2 和轻弹簧为系统,则由于弹性力是保守内力,系统在整个过程中满足机械能守恒条件,即
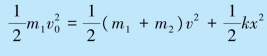
联立以上两式,得
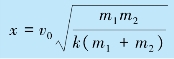
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




