动量守恒定律及其应用

如果质点系所受外力的矢量和为零，即

则由质点系动量定理的微分形式（3.29）可以得到

上式表示，在合外力为零的情况下，质点系的总动量保持不变.这个结论叫做动量守恒定律.

在处理具体问题时，可使用动量守恒在直角坐标系的分量式：

在应用动量守恒定律时应注意以下几点：

（1）由于动量是矢量，故系统的总动量不变是指系统内各物体动量的矢量和不变，而不是指其中某一个物体的动量不变.此外，各物体的动量还必须相对于同一惯性参考系.

（2）有时系统所受外力的矢量和不等于零，但与系统的内力相比较，外力远小于内力，这时可以忽略外力对系统的作用，认为系统的动量是守恒的.例如碰撞、爆炸、打击等类问题.

（3）如果系统所受的合外力不等于零，但合外力在某个坐标轴上的分矢量却等于零.此时系统的总动量虽然不守恒，但在该坐标轴的分动量却是守恒的.

（4）动量守恒定律具有普适性.动量守恒定律虽然是从宏观物体运动规律导出的，但近代的科学实验和理论分析都表明：在自然界中，大到天体间的相互作用，小到质子、中子、电子等微观粒子间的相互作用都遵守动量守恒定律；而在原子、原子核等微观领域中，牛顿运动定律却不适用.

（5）应用动量守恒定律时，只要求作用于系统的合外力等于零，而不必知道系统内部质点间相互作用的细节.

例3.9　设有一静止的原子核，衰变辐射出一个电子和一个中微子（“基本”粒子的一种）后成为一个新的原子核.已知电子和中微子的运动方向相互垂直，且电子的动量为1.2×10-22 kg·m/s，中微子的动量为6.4×10-23 kg·m/s.问新的原子核的动量的值和方向如何？

解　以pe、pν 和pN 分别代表电子、中微子和新的原子核的动量，且pe 与pν 相互垂直，如图3.11 所示.在原子核衰变的短暂时间内，粒子间的内力远大于外界作用于该粒子系统上的外力，故粒子系统在衰变前后的动量是守恒的.考虑到原子核在衰变前是静止的，所以衰变后电子、中微子和新原子核的动量之和亦应等于零，即

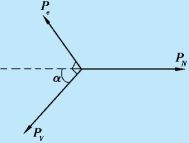
图3.11　例3.9 用图

由于pe 与pν 相互垂直，有

图中的α 角为(www.xing528.com)

宇宙飞船、航天飞机、人造飞船以及导弹的发射，都离不开推力强大的火箭.运载火箭的发射反映了当代科技水平的综合技术.我国是发明火箭最早的国家，约在公元9、10 世纪，我国就开始把火药用到军事上.1232 年，已在战争中使用了真正的火箭.这里简略地介绍火箭飞行原理，它是动量守恒定律的重要应用之一.

火箭（即系统）在发射和飞行过程中，自身携带的燃料（液化氢）在氧化剂（液化氧）的作用下急剧燃烧，生成炽热气体并以高速向后喷射，致使火箭主体获得相前的动量.在时刻t，火箭的质量（包括火箭主体的质量和所携带的燃料）为m，相对于惯性系（如地面）的速度为v；在其后t 到t+dt 时间内，火箭喷出了质量为的气体（由于质量m 是随t 的增加而减小的，所以dm 具有的是负值），喷出的气体相对于火箭的速度为u，使火箭的速度增量了dv.参见图3.12.一枚火箭在外层高空飞行时，那里的空气阻力和重力的影响可以忽略不计，那么系统的动量是守恒的，于是有

*运载火箭的运动

图3.12　运载火箭

考虑到v 与u 的方向相反，以及，并取v 的方向为正方向，则上式可写为

化简并略去二阶微分项dmdv 后，得

如设燃气相对于火箭的喷射速度u 是一常量，火箭开始飞行时速度为零，质量为m0，燃料烧尽时，火箭剩下的质量为m，将上式积分可得式中m0/m 称为火箭的质量比.可见，火箭的质量比越大，燃气的喷射速度越大，火箭获得的速度也就越大.

由式（3.37）可以看出，要提高火箭的速度，可采用提高喷气速度和质量比的办法.但这两种办法目前在技术上都比较困难，喷气速度用液氧可达到4 km/s，由此求出的火箭速度为11 km/s.在地面发射时因受地球引力和空气阻力的影响，火箭速度只有7 km/s.所以一般都采用多级火箭来提高速度.下面简述三级火箭.

若质量比用符号N 表示，则第一、二、三级火箭的质量比可分别为N1=m0/m1，N2=m1/m2，N3=m2/m3，那么，由式（3.37）可得各级火箭中燃料烧尽后，火箭的速率分别为

所以，第三级火箭中的燃料烧尽后，火箭的速率为

若火箭燃气的喷射速度u=2.5 km/s ，每一级的质量比分别为N1=4，N2=3，N3=2，由上式可算得v3=7.93 km/s.这个速度已达到人造卫星的入轨速度.实际上，上述计算只是一种估算.若计及燃料用完后脱落的储存燃料容器的质量，计算还要复杂得多.