大学物理学（上册）：质点系动量定理

本书之前讨论的基本上是单个物体的平动或质点的运动，其情况比较简单.当研究由许多质点组成的系统时，其情况就复杂得多.质点系内各个质点之间的相互作用，称为内力，系统外物体对系统内质点所施加的力，称为外力.一般来说，凡是力和它的反作用力成对地出现在质点系之内，这种力就是内力；力出现在质点系内，但其反作用力却作用在系统外的物体上，则是外力.

1）质心

在研究质点系时，质心是个很重要的概念.将一段绳子团起来，然后斜抛出去，不难想象，绳子上各点的运动轨迹是十分复杂的.但是，我们会发现一个特殊点，它的运动轨迹是抛物线.这个特殊点就是质点系的质心.

质心是与质点系的质量分布有关的一个代表点，它的位置表示质点系质量分布的中心.如果用mi 和ri 表示系统中第i 个质点的质量和位矢，用rC 表示质心的位矢，则质心位置的三个直角坐标定义为

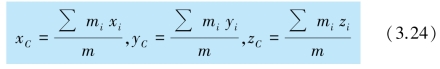
式中m=∑mi 为质点系的总质量.

质心位置表示成矢量式为

如果质点系的质量是连续分布的，则求质心位置时就要把求和改为积分，即

对应的三个直角坐标为

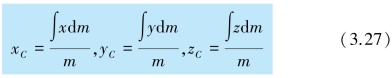
从以上质心位置矢量的表达式可以看到，选择不同的坐标系，质心的坐标值不同.但是，质心相对于质点系的位置是不变的，它完全取决于质点系的质量分布.对于质量分布均匀、形状对称的物体，质心位于物体的几何中心.对于不太大的实物，不必考虑各处的重力加速度差异时，质心与重心重合.

例3.7　求半径为R、顶角为2α 的均匀圆弧的质心.

解　选择x 轴沿圆弧的对称轴，圆心O 为坐标原点，如图3.9 所示.在这种情形下，质心应处于x 轴上.设圆弧的线密度为λ，则长度为dl 的线元的质量为dm=ρRdθ，线元的坐标为x=R cos θ.根据式（3.27），圆弧质心的坐标为

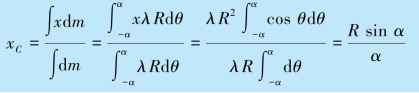
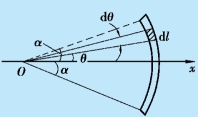
图3.9　例3.7 用图

2）质点系的动量定理

前面讨论的动量定理是描述一个质点在运动中动量的变化规律.而在很多实际情形中，所涉及的是彼此相互作用的多个质点的运动，即质点系的运动问题.下面就来介绍质点系在力的作用下动量的变化规律.

一个由n 个质点组成的质点系，在一般情况下，每个质点既受到外力作用，也受到内力作用.假设第i 个质点在初始时刻的动量为mi vi0，所受来自系统以外的合外力为Fi，同时也受到系统内其他质点的作用力，分别为到时刻t，动量变为mivi，对应的运动方程为

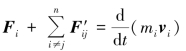
系统内其他质点的情形依次类推.将n 个质点对应的运动方程相加，得

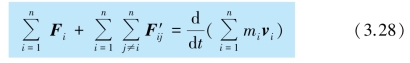
式中表示，i和j都从1 到n 变化所得的各项相加，但除去i = j 的那些项，即除去各项.

根据牛顿第三定律，系统内各质点间的作用力必然是成对出现的相互作用力，因此(www.xing528.com)

所以，式（3.28）中等号左边的第二项等于零，故有

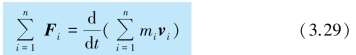
如果外力的作用时间从t0 到t，则对上式积分可得

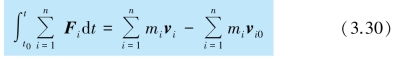
式中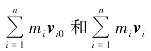分别表示质点系在初状态和末状态的总动量.可见式（3.30） 表明，在一段时间内，作用于质点系的合外力的冲量等于质点系动量的增量.这个结论称为质点系动量定理，式（3.29） 称为质点系动量定理的微分形式.

质点系动量定理还表达了这样一个事实：系统的内力不会改变系统的总动量，系统总动量的变化完全是外力作用的结果.不论是保守力还是非保守力，只要是作为内力出现，都不会改变质点系的总动量.

如同质点的动量定理一样，在处理问题时，在直角坐标系中使用质点系动量定理的分量形式

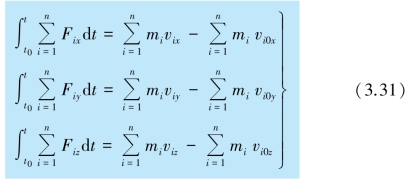
上式表明，合外力在某一方向的冲量等于该方向上质点系总动量的分量的增量.

3）质心运动定理

当质点系的各质点在空间运动时，质点系质心的位置也要发生变化，并且遵从一定的规律.将质心位置矢量定义式（3.25）的右边变形为

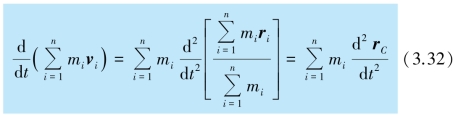
式中是质点系质心的加速度，用aC表示.进而由式（3.29）和式（3.32）可得

上式表明，质点系的质心的运动与这样一个质点的运动具有相同的规律：该质点的质量等于质点系的总质量，作用于该质点的力等于作用于质点系的合外力.这一结论称为质心运动定理.不管物体的质量如何分布，也不管外力作用在物体的什么位置上，质心的运动就像物体的全部质量都集中于此，而且所有外力也都集中作用其上的一个质点的运动一样.

例如一枚炸弹在自由落体过程中爆炸，它的碎片向四面八方飞散，由于爆炸力是内力，不能改变炸弹质心运动，所以炸弹的质心任按原来的自由落体运动.质心运动定理表示的是质点系作为一个整体的运动规律，这一规律是由质心的运动状态来表述的，但是它不能给出各质点围绕质心的运动和系统内部的相对运动.

例3.8　设有一质量为2m 的弹丸，从地面斜抛出去，它飞行在最高点处爆炸成质量相等的两个碎片，如图3.10 所示.其中一个碎片竖直自由下落，另一个碎片水平抛出，它们同时落地.试问第二个碎片落地点在何处？

解　考虑弹丸为一系统，空气阻力略去不计.爆炸前后弹丸质心的运动轨迹都在同一抛物线上，也就是说，爆炸以后两碎片质心的运动轨迹仍沿爆炸前弹丸的抛物线运动轨迹.如取第一个碎片的落地点为坐标原点O，水平向右的轴为Ox 轴正向.设m1 和m2 分别为第一个碎片和第二个碎片的质量，且m1=m2=m；x1 和x2 为两碎片落地时距原点的距离，xC 为两碎片落地时它们的质心距原点O 的距离.由图可知x1=0，于是，从式（3.24）可得

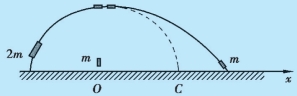
图3.10　例3.8 用图

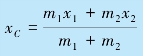
整理得

即第二个碎片的落地点与第一个碎片落地点的水平距离为碎片的质心与第一个碎片水平距离的两倍.这个问题虽也可以用第一章的质点运动学方法来求解，但要烦琐得多.