质点动量定理-大学物理学上册

现在，我们从牛顿第二定律的微分形式dp=Fdt 出发，考察力的时间累积效应.为此，将上式从t1 到t2 这段有限时间内进行积分，得

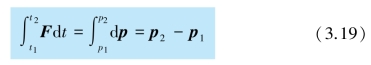
左侧积分力的冲量，表示外力在这段时间内的累积，用I 表示，国际单位制中的单位为N·s，与动量的单位相同.冲量定义为

于是式（3.19）可表示为

上式的物理意义是：在给定时间间隔内，外力作用在质点上的冲量，等于质点在此时间内动量的增量.这就是质点的动量定理.一般来说，冲量的方向并不与动量的方向相同，而是与动量增量的方向相同.

考虑到在低速运动的牛顿力学范围内，质点的质量可视为不变的，则式（3.21）也可以表示为

因为动量和冲量都是矢量，所以质点的动量定理是一个矢量方程.在处理具体问题时，常使用它的分量式.在平面直角坐标系中，其分量式为

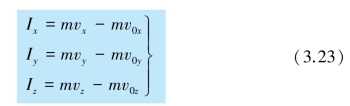
上式表明，冲量在某个方向的分量等于该方向上质点动量分量的增量，冲量在任一方向的分量只能改变自己方向的动量分量，而不能改变与它相垂直的其他方向的动量分量.

下面对动量定理作几点说明：

（1）即便力F 在运动过程中时刻改变着，并且物体的速度方向时刻改变，动量定理却总是成立的，即不管物体在运动过程中动量如何变化，冲量的大小和方向总等于物体始、末动量的矢量差.这便是应用动量定理解决问题的优点所在.

（2）动量定理在处理碰撞和冲击问题时很方便.在这类问题中，作用于物体的力的作用时间极短、数值很大而且变化很快，称为冲力.因为冲力是变力，它随时间变化的关系比较难确定，直接计算冲量也就比较困难.但是，可以测出物体在碰撞或冲击前后的动量，根据动量定理由动量变化来确定冲量.此外，如果还能测定冲力的作用时间，就可对冲力的平均值作出估算.如图3.7 所示，F 表示变力F（其方向是一定的）的平均值，定义为令F 横线下的面积和变力F 曲线下的面积相等，即F 和作用时间t2-t1 的乘积等于变力F 的冲量.尽管这个平均值不是冲力的确切描述，但在不少实际问题中，这样的估算已经足够了.

（3）前面已经提到，在牛顿力学中，描述物体运动必须选用惯性系.对于不同的惯性系，物体的速度不同，动量也随之不同，即动量具有相对性.但在不同的惯性系中，速度的变化是相同的，即在不同惯性系中，动量变化相同，因此动量定理在不同惯性系中具有相同的形式，动量定理具有不变性.也就是说，动量定理在所有惯性系中都适用.(www.xing528.com)

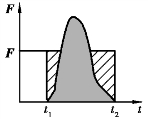
图3.7　冲力的平均值

例3.6　一长为l、密度均匀的柔软链条，其单位长度的质量为λ.将其卷成一堆放在地面上，如图3.8 所示.若手握链条的一端，以匀速v 将其上提.当链条一端被提离地面高度为y 时，求手对链条的提升力.

解　取地面为惯性参考系，地面上一点为坐标原点O，竖直向上为轴的Oy 轴正向.以整个链条为一系统.设在时刻t，链条一端距原点的高度为y，其速率为v.由于在地面部分的链条的速度为零，故在时刻t，链条的动量为

链条的动量随时间的变化率为

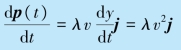
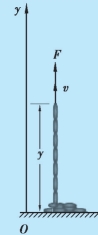
图3.8　例3.6 用图

作用于整个链条上的外力，有手的提力F、重力λyg 和λ（l-y）g 以及地面对（l-y）长链条的支持力FN.由牛顿第三定律知FN 与λ（l-y）g 的大小相等、方向相反，所以系统所受的合外力为

由以上两式得

进而得F=λv2+λyg.