万有引力、重力与弹性力在大学物理学中的做功特点

1）万有引力做功

如图3.3 所示，有两个质量为M 和m 的质点，假设质点M 固定不动（M≫m），质点m 经任一路径由点P 运动到点Q.取M 的位置为坐标原点，P、Q 两点对M 的距离分别为rP 和rQ.设在某一时刻质点m 距质点M 的距离为r，对应的位矢为r，此时质点m 受到质点M 的万有引力为

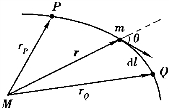
图3.3　万有引力做功

式中er 为位矢r 的单位矢量.当m 沿路径移动位移元dl 时，万有引力所做的功为

所以，质点m 从点P 沿任一路径到达点Q 的过程中，万有引力做的功为

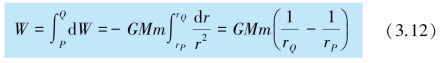
上式表明，当质点的质量M 和m 给定时，万有引力的功只取决于质点m 的起始和终了的位置，而与所经过的具体路径无关.

2）重力做功

设一质量为m 的质点，在重力作用下经任一路径由点P 运动到点Q.若质点在平面内运动，取地面上某一点为坐标原点O，建立如图3.4 所示的坐标系，设两点距地面的高度分别为yP 和yQ.质点所受重力为G=-mgj.当该质点沿路径移动位移元dl 时，重力做的功为

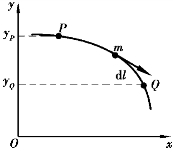
图3.4　重力做功

所以，质点m 从点P 运动到点Q 的过程中，重力做的总功为

上式表明，重力做功只与质点的起始和终了位置有关，而与所经过的具体路径无关.

3）弹性力做功

如图3.5 所示，一放置在光滑平面上的弹簧，劲度系数为k，与其相连的物体质量为m.设弹簧未发生形变时物体位于点O，称为平衡位置，并令该点为所建立坐标系的坐标原点.当弹簧沿x 轴被拉长，物体的位移为x 时，弹簧的伸长量也为x.根据胡克定律，在弹性限度内，弹簧的弹性力F 与弹簧的伸长量x 之间存在如下关系

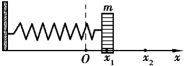
图3.5　弹力做功

在弹簧位移为dx 时，弹性力做的元功为

所以，在弹簧的伸长量由x1 变动x2 时，弹性力所做的功为

上式表明，对在弹性限度内具有给定劲度系数的弹簧来说，弹性力所做的功只由弹簧起始和终了的位置有关，而与弹性形变的具体过程无关.

4）保守力与非保守力(https://www.xing528.com)

从上述讨论可以看出，万有引力、重力和弹性所做的功只与质点（或弹簧）的始末位置有关，而与具体路径无关，具有这种特点的力叫做保守力.保守力还有电荷间相互作用的库仑力，以及原子间相互作用的分子力.保守力做功只与始末位置有关，如果物体始末位置相同，保守力对其做功必为零.因此，对于保守力：物体沿任意闭合路径绕行一周，保守力对它所做的功恒等于零，即

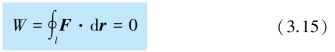
上式为保守力做功特点的数学表达式.

日常生活中常见的摩擦力做功不具有保守力的特点，它所做的功与路径有关，路径越长，摩擦力做的功就越大.具有这种特点的力叫做非保守力.除摩擦力外，磁场对电流作用的安培力，以及空气阻力等都是非保守力.

5）势能

因为做功只与物体的始末位置有关，所以对于保守力可以引入与该保守力对应的势能.我们把与物体位置有关的能量称为物体的势能，用Ep 表示.于是上述三个保守力对应的势能分别为

重力势能　Ep=mgy　（以物体位于地面时为重力势能零点）

引力势能　（以两质点相距无限远时为引力势能零点）

弹性势能　（以弹簧处于原长状态时为弹性势能零点）

进而下式成立

上式表明，保守力对物体所做的功在数值上等于物体势能的减少量，或者说成保守力对物体所做的功在数值上等于物体势能增量的负值.

为了加深对势能物理涵义的理解，强调如下几点：

（1）势能是状态函数，也就是说，势能是关于坐标的单值函数，即Ep=Ep（x，y，z）.

（2）势能具有相对性.势能的值与零势能位置的选取有关.虽然原则上说零势能位置的选取是任意的，但习惯上一般选取物体位于地面时为重力势能零点，两物体相距无限远时为万有引力势能零点，弹簧处于自然状态时为弹性势能零点.

（3）势能属于存在保守力作用的物体组成的系统.势能是因系统内各物体间有保守力作用而存在的，所以抛开系统谈单个物体的势能没有意义.例如重力势能是属于地球和物体所组成的系统的，在不至于造成混淆的情况下才不提及地球而仅说某物体的重力势能.

6）势能曲线

当零势能的位置确定后，势能便仅是物体所在位置的坐标的函数.依此函数画出的势能随坐标变化的曲线，称为势能曲线.利用该曲线，可方便地讨论物体在保守力作用下的运动.前面提到的三种势能对应的势能曲线如图3.6 所示.

在系统的总能量E=Ek+Ep 保持不变的条件下，在势能曲线图上，可用一平行于横坐标轴的直线来表示它，进而系统在每一位置时的动能的大小（Ek=E-Ep）就可以方便地在图上标示出来.由于动能不可能为负值，只有符合Ek≥0 的运动才可能发生.所以，根据势能曲线的形状可以讨论物体的运动.例如，在图3.6 中，表示总能量的直线与势能曲线相交于A、B 两点，这表明质点只能在AB 的范围内运动，而且在A、B 两点，质点的动能为零，速度也为零.

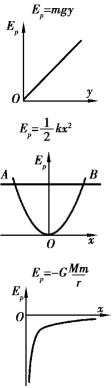
图3.6　势能曲线

利用势能曲线，还可以判断物体在各个位置所受保守力的大小和方向.将式（3.16）写成微分形式

当系统内的物体在保守力F 作用下，沿Ox 轴发生位移dx时，保守力所做的功为

θ 为F 与Ox 轴正方向的夹角.比较以上两式，得

上式表明：保守力沿某坐标轴的分量等于势能对此坐标的导数的负值.重力、万有引力和弹性力对于上式都成立.