非惯性系中的惯性力及应用分析

在非惯性系中牛顿运动定律不再成立，所以不能直接用牛顿运动定律处理力学问题.若仍然希望能用牛顿运动定律处理这些问题，以便在形式上利用牛顿定律去分析问题，则必须引入一种作用于物体上的惯性力.惯性力不同于真实的力，是在非惯性系中来自参考系本身的加速效应的力.惯性力既没有施力物体，也不存在它的反作用力.下面分三种情况讨论：

1）直线加速参考系中的惯性力

若某参考系相对于惯性系作变速直线运动，且各坐标轴的方向保持不变，该参考系就是直线加速参考系.如图2.1 所示，固定在车厢里的一个光滑桌面上放着一个滑块.当车厢以加速度a 由静止开始做直线运动时，在地面参考系观察.滑块A 在水平方向上不受任何力的作用，所以保持静止，这与牛顿运动定律的结论相符.但在车厢参考系中观察，在水平方向上不受力的滑块以加速度-a 在桌面上运动，这显然与牛顿运动定律相违背.为在直线加速参考系中应用牛顿运动定律处理问题，可引入惯性力

图2.1　车厢系统

上式表示，在直线加速参考系中，惯性力的方向与非惯性系相对于惯性系的加速度的方向相反，大小等于所研究物体的质量与加速度的乘积.在图2.1 的例子中，若以车厢为参考系，滑块受到惯性力Fi=-ma 的作用.当车厢以加速度a 向右运动时，滑块由于受到向左的惯性力的作用而以加速度a 向左运动.

例2.6　一质量为m 的人，站在电梯中的磅秤上，当电梯以加速度a 匀加速上升时，磅秤上指示的读数是多少？试用惯性力的方法求解.

解　取电梯为参考系.已知这个非惯性系以a 的加速度相对地面参考系运动，与之相应的惯性力的大小为F惯=-ma，符号表示惯性力的方向与加速度的方向相反.从电梯这个非惯性系看来，人除受到重力G（方向向下）和磅秤对他的支持力FN（方向向上）之外，还要另加一个F惯.此人相对于电梯是静止的，则以上三个力必须恰好平衡，即

于是FN=G+F惯=m（g+a）

由此可见，磅秤上的读数（根据牛顿第三定律，磅秤的读数是人对秤的正压力，而正压力和FN 是一对大小相等的作用力与反作用力）不等于物体所受的重力G.当加速上升时，FN>G；加速下降时，FN<G.前一种情况叫作“超重”，后一种情况叫作“失重”.尤其在电梯以重力加速度下降时，失重最严重，磅秤上的读数将为零.

2）匀速转动参考系中的惯性力

相对于某惯性系作匀速圆周运动的参考系也为非惯性系.如图2.2 所示.长度为R 的细绳的一端系一质量为m 的小球，另一端固定于圆盘的中心.当圆盘以匀角速度ω 绕通过盘心并垂直于盘面的竖直轴旋转时，小球也随圆盘一起转动.若以地面为参考系，由细绳的张力所提供的向心力FT 使小球做圆周运动，这符合牛顿运动定律，且

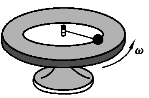
图2.2　旋转圆盘

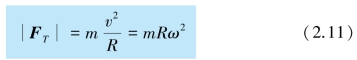
若以圆盘这个非惯性系为参考系，小球受到细绳的拉力作用，却是静止的，这不符合牛顿运动定律.为了应用牛顿运动定律，可设想小球除了受细绳的张力FT 的作用外，还受到惯性力Fi 的作用，Fi 可以表示为

式中r 是从转轴向质点（在此是小球）所引的有向线段，且与转轴相垂直.由于这种惯性力的方向总是背离轴心的，所以称为惯性离心力（inertial centrifugal force）.引入惯性离心力后，小球受力满足下面的关系了

(www.xing528.com)

图2.3　旋转圆盘俯视图

所以小球保持静止，牛顿运动定律依然成立.于是可以得到这样的结论：若质点在匀速转动的非惯性系中保持静止，则作用于该质点的外力与惯性离心力的合力等于零.

*3）科里奥利力

通过上面讨论，可知在匀速转动的非惯性系中保持静止的物体，要受到惯性离心力的作用.如果物体相对于该匀速转动参考系在运动，作用于物体的除了惯性离心力以外，还有另一种惯性力，这种惯性力称为科里奥利力.下面就科里奥利力的产生和作用做如下分析.

现设想，一个带有径向光滑沟槽的圆盘，以匀角速度ω 绕通过盘心并垂直于盘面的固定竖直轴O 转动，处于沟槽中的质量为m 的小球以速度u 沿沟槽相对于圆盘做匀速运动，如图2.3所示.在圆盘上的观察者看到，经过Δt 时间，小球沿沟槽从点A到达点B.而在地面上的观察者却看到，小球同时参与了两个运动：以速度u 相对于圆盘的运动和随圆盘的转动.如果只有圆盘的转动，在Δt 时间内圆盘转过了Δθ 角，小球到达点A′；如果只有小球沿沟槽的运动，小球只能到达点B.根据位移合成的平行四边形定则，取A′B″平行于AB，经过Δt 时间，小球应该到达点B″.而实际上小球是沿曲线AB′到达了点B′，即比合成的结果多运行了B″B′的距离.这说明小球的运动在垂直于半径的方向存在一种横向加速度，致使小球在Δt 时间内多运行了B″B′的距离.这种加速度之所以存在，显然是由于随着小球离开盘心距离的增加，垂直于半径的横向速度在不断增大的缘故.若把这种加速度表示为at，则有

从图2.3 中所画的几何关系中可以得到

比较以上两式，可以得到横向加速度at 的大小为at=2uω，只有力的作用才能使物体获得加速度，使小球获得横向加速度at 的力记为Ft.根据牛顿第二定律，其大小为Ft=2muω.Ft 的方向在图2.3 中是垂直于半径指向右的.这个力显然是由沟槽壁施加于小球的.

在圆盘这个匀速转动参考系中的观察者看到，尽管有力Ft 的作用，小球仍然沿沟槽做匀速直线运动.这表明，在垂直于小球的运动方向上还受到一个与Ft 相平衡的力，将这个力记为Fc，则

所以力Fc 的大小为

Fc 方向与Ft 相反，即垂直于半径指向左.这个力就是科里奥利力.

可以证明，在一般情况下科里奥利力应由下式表示

在上式中，角速度ω 的方向可以这样确定：让右手四指沿转动方向围绕转轴而弯曲，拇指所指的方向就是角速度的方向.上式表明，科里奥利力Fc 与u、ω 三者的方向满足右螺旋关系.

总之，在匀速转动的非惯性系中分析力学问题时，一般情况下需要同时考虑惯性离心力和科里奥利力.在地球这个匀速转动的非惯性系中，科里奥利力的作用也明显地表现出来.赤道附近的空气因受热而上升，并向两极推进，两极附近的冷空气则沿地面向赤道流动.在北半球，从北向南流动的气流所受科里奥利力的方向是从东向西的，这就形成了所谓东北信风，而在南半球则形成东南信风.在北半球地面上运动的物体，所受科里奥利力总是指向前进方向的右侧；在南半球地面上运动的物体，所受科里奥利力总是指向前进方向的左侧.所以北半球的河流，右岸被冲刷得比较厉害，常呈陡峭状.单行线铁路的右轨被磨损得比较严重.而在南半球，情况与此相反.