已知作用于质点上的力和初始条件，求质点的运动规律（v，r）.这种情况，一般需用积分方法求解二阶微分方程.下面仅就一维直线运动的情况分三类讨论：
①力是时间的函数，即F=F（t），此时，质点的动力学方程为
，分离变量后积分，并代入初始条件，即可求得v=v（t）.利用
再分离变量积分，并代入初始条件，即可求得x=x（t）.
例2.3 质量为m 的质点在周期性外力F=F0cos ωt 的作用下开始沿x 轴运动，其中F0、ω 均为常量.设t=0 时质点静止于坐标原点，求质点的速度、位置与时间的关系.
解 由质点的动力学方程
分离变量后得
将上式两边分别积分，并注意到t=0 时，v0=0，则有
积分上式得
将
代入上式，并注意到t=0 时，x0=0，分离变量后积分得
②力是坐标的函数，即F=F（x），此时，质点的动力学方程为
，利用关系式
作变量替换，上述方程即可变为
，对该式积分，并代入初始条件：x=x0 时，v=v0，即可求出v 随x 变化的关系式v=v（x）.
例2.4 一质点沿x 轴运动，所受的力和坐标的关系为F=F0-kx，其中F0、k 均为常量，质点在x=0 处的速度为v0，求质点的速度和坐标的关系.
解 由质点的动力学方程得
将
代入上式，得(www.xing528.com)
分离变量得
对上式两边积分，并代入初始条件：x=0，v=v0，则有
解得
③力是速度的函数，即F=F（v）.这时，质点的动力学方程为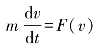
，分离变量，得出微分方程
，然后等式两边积分，并代入初始条件：t=0 时，v=v0，则可解出速度与时间的函数关系式v=v（t）.根据题设条件再积分，便可求出质点的位置坐标x=x（t）.有时也可直接将
代入动力学方程来求质点的位置坐标，以简化问题的计算.
例2.5 质量为m 的小船在平静的湖面上以速度v0 航行.由于特殊情况，小船突然关机.这时，水的阻力与小船速度之间的关系为F=-bv（b 为常量）.求：（1）船速与时间的关系；（2）小船所能滑行的最大距离.
解 （1）由牛顿第二定律可得小船的动力学微分方程为
分离变量并积分得
解之得
（2）由速度的定义式
得
分离变量并积分得
解之得
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
