【摘要】：设有两个参考系分别为S（Oxyz）和S′（O′x′y′z′），各对应轴相互平行，其中x 和x′轴重合，并且S′系相对于S 系以速度v 沿x 轴做匀速直线运动.计时开始时刻，两坐标原点O 和O′相重合.称坐标系S 为基本坐标系，坐标系S′为运动坐标系.图1.12坐标系S 和S′如图1.12 所示.要找出同一质点P 在S 系和S′系内的坐标关系.设质点P 在S 系和S′系中的位矢分别为r 和r′，并
设有两个参考系分别为S（Oxyz）和S′（O′x′y′z′），各对应轴相互平行，其中x 和x′轴重合，并且S′系相对于S 系以速度v 沿x 轴做匀速直线运动.计时开始时刻，两坐标原点O 和O′相重合.称坐标系S 为基本坐标系，坐标系S′为运动坐标系.
图1.12 坐标系S 和S′
如图1.12 所示.要找出同一质点P 在S 系和S′系内的坐标关系.设质点P 在S 系和S′系中的位矢分别为r 和r′，并以R 代表S′系原点O′相对S 系原点O 的位矢.从图中可见事实上，上式成立是有条件的.先从S 系讨论，它认为r 和R 是自己观测的值，而r′是S′系的观测值.在矢量相加时，各个矢量必须由同一坐标系来测定.所以，只有S 系观测得
的矢量值确实与r′相同，对S 系来说上式才成立.由此可见，上式成立的条件是：空间两点的距离不管从哪个坐标系测量，结果都应相同.这一结论叫做空间绝对性.
其次，物体运动的研究，不仅涉及空间，还要涉及时间.同一运动所经历的时间，由S 系观测为t，由S′系观测为t′.在宏观物体低速运动情况下，二者是近似相同的，即
这表明时间与坐标系无关，这个结论叫做时间绝对性.因此有(www.xing528.com)
上述关于时间和空间的两个结论，即长度测量的绝对性和同时性测量的绝对性，构成了经典力学的绝对时空观，这种观点是和大量日常经验相符合的.但是，只有在两个惯性系之间相对运动速度的大小远小于真空中的光速的情况下，这两种绝对性才近似和实际相符.两个惯性系之间相对运动速度的大小和光速接近的情形在狭义相对论中再作讨论.
综上所述，可以得出这两个坐标系间的伽利略（坐标）变换式：
或者写成
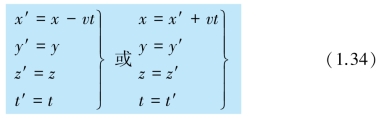
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
