大学物理学（上册）：抛体运动

从地面上某点向空中抛出一物体，它在空中的运动就叫抛体运动.抛体运动是一种平面曲线运动.在研究抛体运动时，通常都取抛射点为坐标原点，而沿水平方向和竖直方向分别引x 轴和y轴（图1.10）.

从抛出时刻开始计时，则t=0 时，物体位于原点.以v0 表示物体的初速度，以θ 表示抛射角，则v0 在Ox 轴和Oy 轴上的分量为

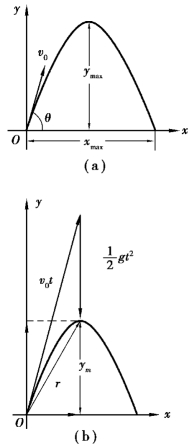
图1.10　抛体运动

物体在整个运动过程中的加速度为

利用这些条件，可求出物体在空中任意时刻的速度为

由可得物体的运动学方程为

上式就是抛体运动方程的矢量形式，表明抛体运动是由沿Ox 轴的匀速直线运动和沿Oy 轴的匀变速直线运动叠加而成的.

对任何一个矢量，通常都有许多种分解方法，同样也存在着多种多样的叠加方法.在图1.10（b）中，画出了以位矢r 为一边的矢量三角形叠加法.为了看出这点，将式（1.25）重新改写如下：

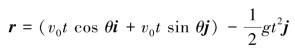
即

这就是说，抛体运动还可看作由沿初速度方向的匀速直线运动和沿竖直方向的自由落体运动叠加而成.

由式（1.25）的两个分量式中消去t，即得抛体的轨迹方程为

(www.xing528.com)

这是一条抛物线，所以抛体运动又叫抛物线运动.令式中y=0，求得抛物线与Ox 轴的一个交点的坐标为

这就是抛体的射程.显然，具有一定初速度v0 的物体，要想射得远，可令sin 2θ=1，亦即在θ=45°时，射程为最大.

根据高等数学中求函数极值的方法，将式（1.27）对x 求导，并令dy/dx=0，由此得将它代入式（1.27），即得物体在飞行中所能达到的最大高度（射高）为

应该指出，上述结论是在忽略空气阻力的理想情况下得到的，在实际应用中只有空气阻力比较小的情况下才近似符合实际.初速度大了，空气阻力不能忽略，实际飞行的曲线与抛物线将有很大差别.在弹道学中，除以上述式子为基础外，还要考虑空气阻力、风向、风速等的影响加以修正，才能得到抛体运动与实际相符的结果.

例1.3　如图1.11 所示，一超音速歼击机在高空点A 时的水平速率为1 940 km/h，沿近似于圆弧的曲线俯冲到点B，其速率为2 192 km/h，所经历的时间为3 s.设圆弧AB 的半径约为3.5 km，且飞机从A 到B 的俯冲过程可视为匀变速圆周运动.若不计重力加速度的影响.求：（1）飞机在点B 的加速度；（2）飞机由点A 到达点B 所经历的路程.

解　（1）如图1.11 所示，在点B 作一自然坐标系，切向单位矢量为et，法向单位矢量为en.由于飞机在A、B 之间作半径为3.5 km 匀变速率圆周运动，所以和角加速度的值α 均为常量.飞机在点B 的切向加速度的值为

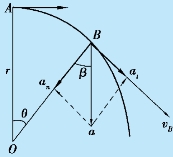
图1.11　例1.3 用图

有　

得　

代入数值，得飞机在点B 的切向加速度为at=22.3 m/s2

飞机在点B 的法向加速度的值为

故飞机在点B 的加速度的值为

加速度与切向单位矢量间的夹角为

（2）在时间t 内，位矢所转过的角度为

式中ωA 是飞机在点A 的角速度.故在此时间内，飞机经过的路程为s=rθ=1 722 m.